電路設計中拉普拉斯變換的應用

拉氏變換里的S是復變函數里最為基礎的一個符號，數學題做了這么多，考分也不低，但如果在多年的電路設計中用不上的話，豈不是對不起寶貴的青春了。

要用好拉氏變換，先了解S的物理含義和其用途。信號分析有時域分析、頻域分析兩種，時域是指時間變化時，信號的幅值和相位隨時間變化的關系;頻域則是指頻率變化時，信號的幅值和相位隨時間變化的關系;而S則是連接時域與頻域分析的一座橋梁。

在電路中，用到的阻性用R表示;用到的感性特性和容性特性，分別用SL和1/SC表示，然后將其看成一個純粹的電阻，只不過其阻值為SL(電感)和1/SC(電容);

其他特性(如開關特性)則均可通過畫出等效電路的方式，將一個復雜的特性分解成一系列阻性、感性、容性相結合的方式。并將其中的感性和容性分別用SL和1/SC表示。

然后，就可以用初中學過的電阻串、并聯阻抗計算的方式來進行分壓、分流的計算，這當然很簡單了。計算完后，最后一定會成一個如下四種之一的函數：

Vo=Vi(s)--------------------(1)

Io=Vi(s)--------------------(2)

Vo=Ii(s)--------------------(3)

Io=Ii(s) --------------------(4)

下一步，如果是做時域分析，則將S=d/dt代入上述1-4其中之一的式子中，隨后做微分方程的求解，則可求出其增益對時間的變化式 G(t);

而如果做的是頻域分析，則將S=jw代入上述1-4其中之一的式子中，隨后做復變函數方程的求解，則可求出其增益對時間的變化式 G(w)、和相位對頻率的變化式 θ(w);

至于求出來時域和頻域的特性之后，您再想把數據用于什么用途，那就不是我能關心得了的了。

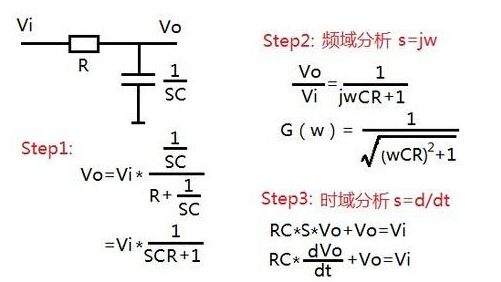
下面舉一簡單例子說明。