ARM處理器NEON編程及優化技巧——矩陣乘法的實例

矩陣

本節將介紹如何用NEON有效的處理一個4x4的矩陣乘法運算，這種類型的運算經常用于3D圖形，我們認為這些矩陣在內存里是按照列為主排列的，這是按照OPENGL-ES的通用格式。

矩陣乘法算法

我們首先看一下矩陣乘法的計算方式，計算的展開，用NEON指令來進行子操作過程。

圖1. 以列為主的矩陣乘法運算

由于數據是按照列序存儲的，因而矩陣乘法就是把第一個矩陣的每一列乘以第二個矩陣的每一行，然后把乘積結果相加。乘累加結果 作為結果矩陣的一個元素。

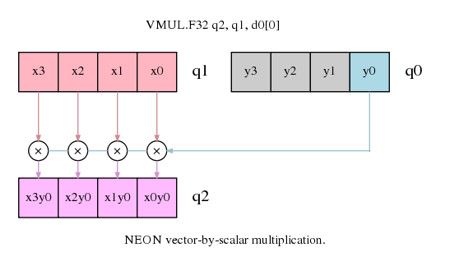
圖2. 矩陣乘法中的向量乘以標量的運算

假設每列元素在NEON寄存器中表示為一個向量，那么上述的矩陣乘法就是一個向量乘以標量的運算，而后續的累加也同樣可以同向量乘以標量的累加指令實現。因為我們的操作是在第一個矩陣的列，然后計算列的結果，讀列元素和寫列元素都是線性的加載和存儲操作，不需要interleave的加載和存儲操作。

代碼

浮點運算版本

首先看一個單精度浮點的矩陣乘法實現。首先加載矩陣元素到NEON寄存器，然后按照列序做乘法，用VLD1做線性的加載數據到NEON寄存器，用VST1把計算結果保存到內存。

vld1.32 {d16-d19}, [r1]!            @ 加載矩陣0的上8個元素 

vld1.32 {d20-d23}, [r1]!            @ 加載矩陣0的下8個元素 

vld1.32 {d0-d3}, [r2]!              @ 加載矩陣1的上8個元素 

vld1.32 {d4-d7}, [r2]!              @ 加載矩陣1的下8個元素 

NEON有32個64位寄存器，因而加載所有的輸入矩陣元素到16個64-bit寄存器，我們仍然有16個64位寄存器做后續的處理。

D和Q寄存器

多數的NEON指令有兩種方法來訪問寄存器組：

• 作為32個雙字寄存器，64-bit位寬，命名為d0-d31
• 作為16個四字寄存器，128-bit位寬，命名為q0-q15

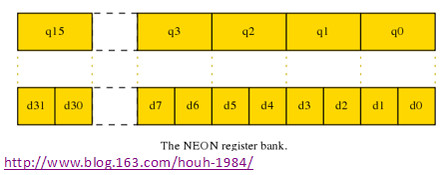
圖3. NEON寄存器組

這些寄存器中一個Q寄存器是一對D寄存器的別名，如Q0是d0和d1寄存器對的別名，寄存器中的值可以用兩種方式訪問。這種實現方式很類似C語言里的union聯合的數據結構。對于浮點的矩陣乘法，我們會經常使用Q寄存器的表達方式，因為經常會處理4個32-bit的單精度浮點，這對應于128-bit的Q寄存器。

代碼部分

通過以下4條NEON乘法指令能完成一列4個結果：

vmul.f32    q12, q8, d0[0]        @ 向量乘以標量（MUL），矩陣0的第一列乘以矩陣1的每列的第一個元素0 

vmla.f32    q12, q9, d0[1]        @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素1 

vmla.f32    q12, q10, d1[0] @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素2 

vmla.f32    q12, q11, d1[1] @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素3 

第一條指令是圖2中的列元素x0, x1, x2, x3 (寄存器q8)乘以y0 (d0[0])，然后結果保存到q12寄存器。接下來的指令操作類似，就是把第一個矩陣的其他列乘以第二個矩陣的第一列的響應元素，結果累加到寄存器Q12里。需要注意的是標量元素如d1[1]也可以用q0[3]表示，但是可能編譯器如GNU匯編器會不能接受這種方式。

如果我們只需要矩陣乘以向量的運算，如很多3D圖像處理中的那樣，那么此時的計算就結束了，可以把結果向量保存 到內存了，但是為了完成矩陣相乘，還需要完成后面的迭代操作，使用寄存器Q1到Q3的y4到yF的元素。如果定義如下的宏，那么就能簡化代碼結構了：

.macro mul_col_f32 res_q, col0_d, col1_d 

vmul.f32    res_q, q8, col0_d[0]      @向量乘以標量（MUL），矩陣0的第一列乘以矩陣1的每列的第一個元素0 

vmla.f32    res_q, q9, col0_d[1]      @累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素1 

vmla.f32    res_q, q10, col1_d[0] @累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素2 

vmla.f32    res_q, q11, col1_d[1] @累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素3 

.endm 

那么整個4x4的矩陣乘法代碼可能如下：

vld1.32 {d16-d19}, [r1]!            @ 加載矩陣0的上8個元素 

vld1.32 {d20-d23}, [r1]!            @ 加載矩陣0的下8個元素 

vld1.32 {d0-d3}, [r2]!              @ 加載矩陣1的上8個元素 

vld1.32 {d4-d7}, [r2]!              @ 加載矩陣1的下8個元素 

mul_col_f32 q12, d0, d1         @ 矩陣 0 * 矩陣1的第一列 

mul_col_f32 q13, d2, d3         @ 矩陣 0 * 矩陣1的第二列 

mul_col_f32 q14, d4, d5         @ 矩陣 0 * 矩陣1的第三列 

mul_col_f32 q15, d6, d7         @ 矩陣 0 * 矩陣1的第四列 

vst1.32 {d24-d27}, [r0]!            @ 保存結果的上8個元素 

vst1.32 {d28-d31}, [r0]!            @ 保存結果的下8個元素 

定點算法

定點算法計算往往比浮點計算更快，因為往往定點運算可能需要更少的內存帶寬，整數值的乘法也會比浮點算法更為簡單。但是定點算法，你需要很仔細的選擇表示格式來避免溢出或者飽和，這些會影響你的算法最終的精度。定點算法實現的矩陣乘法和浮點算法類似，在本例中，用Q1.14定點格式,但是基本的實現格式基本類似，只是實現中可能需要對結果做一些移位調整。下面是列乘的宏：

.macro mul_col_s16 res_d, col_d 

vmull.s16   q12, d16, col_d[0] @ 向量乘以標量（MUL），矩陣0的第一列乘以矩陣1的每列的第一個元素0 

vmlal.s16   q12, d17, col_d[1] @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素1 

vmlal.s16   q12, d18, col_d[2] @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素2 

vmlal.s16   q12, d19, col_d[3] @ 累加的向量乘以標量（MAC），矩陣0的第二列乘以矩陣1的每列的第二個元素3 

vqrshrn.s32 res_d, q12, #14             @ 把結果右移14位，并把累加結果變成Q1.14定點格式，并飽和運算 

.endm 

比較定點和浮點算法的宏，你會發現如下的主要區別：

• 矩陣元素的值為16位而不是32位，因而用D寄存器來保存4個輸入元素
• 矩陣乘法的結果是把16x16=32位的數據，使用VMULL和VMLAL來吧結果保存到Q寄存器。
• 最終結果也是16位，因而需要把32位累加器結果來得到16-bit的結果，使用VQRSHRN，飽和處理把32位的結果舍入到16位的narrow右移操作。

把數據從32-bits變成16-bits也能有效的處理內存訪問，加載和存儲數據都只需要更少的帶寬。

vld1.16 {d16-d19}, [r1]     @ 加載16個元素到矩陣0 

vld1.16 {d0-d3}, [r2]       @ 加載16個元素到矩陣1 

mul_col_s16 d4, d0                      @ 矩陣0乘以矩陣1的列0 

mul_col_s16 d5, d1                      @ 矩陣0乘以矩陣1的列1 

mul_col_s16 d6, d2                      @ 矩陣0乘以矩陣1的列2 

mul_col_s16 d7, d3                      @ 矩陣0乘以矩陣1的列3 

vst1.16 {d4-d7}, [r0]       @ 保存16個結果元素 

指令重排

我們先展示一下指令重排如何能提高代碼性能。在宏中，臨近的乘法指令會寫入到相同的目標寄存器，這會讓NEON的流水線等待前面的乘法結果完成才能開始下一條指令的執行。如果不使用宏定義，而合理安排指令的次序，把那些相關依賴的指令變成不依賴，這些指令就能并發而不會造成流水線的stall。

vmul.f32    q12, q8, d0[0]              @ rslt col0  = (mat0 col0) * (mat1 col0 elt0) 

vmul.f32    q13, q8, d2[0]              @ rslt col1  = (mat0 col0) * (mat1 col1 elt0) 

vmul.f32    q14, q8, d4[0]              @ rslt col2  = (mat0 col0) * (mat1 col2 elt0) 

vmul.f32    q15, q8, d6[0]              @ rslt col3  = (mat0 col0) * (mat1 col3 elt0) 

vmla.f32    q12, q9, d0[1]              @ rslt col0 += (mat0 col1) * (mat1 col0 elt1) 

vmla.f32    q13, q9, d2[1]              @ rslt col1 += (mat0 col1) * (mat1 col1 elt1) 

... 

... 

用以上的處理方式，矩陣乘法的性能在Cortex-A8處理平臺上性能提升了一倍。從文檔arm.com/help/index.jsp?topic=/com.arm.doc.set.cortexa/index.html" rel="nofollow">Technical Reference Manual for your Cortex core可以看到 各個指令的需要時間以及延遲，有這些延遲周期，能夠更為合理的安排代碼次序，提升性能。