基于穩態的ABSK信號解調模式（一）

0 引言

　　隨著無線通信業務的高速發展，空中的無線電頻譜越來越擁擠，無線頻譜利用率越來越受到重視。經典的二元偏移鍵控，頻譜利用率很低，其中綜合性能較好的2-PSK（BPSK），頻譜利用率也最多只有1 bps/Hz.雖然通過增加信號空間的星座點數可以提高頻譜利用率（如多電平的正交幅度相位調制M-QAM和多相移鍵控調制M-PSK），但處理起來較為復雜，所需的發射功率也要相應增加。

　　與上述調制方式相比，不對稱二元偏移鍵控調制（Asymmetry Binary Shift Keying，ABSK）具有極大優勢，其利用微小的波形差異來分別調制“0”、“1”碼元，使得調制信號能量集中在載頻處，信號帶寬大大縮減，符合工程意義上“超窄帶”的要求 。

　　同時，也正因為“0”、“1”碼元的波形差異微小，給ABSK信號的解調帶來不小困難。經典的濾波理論和常規的濾波器很難滿足要求，美國的H. R. Walker博士發明了所謂“零群時延”晶體帶通濾波器，雖然可實現ABSK信號的解調，但由于采用石英晶體實現，不僅可靠性、穩定性、靈活性和一致性都很差，而且難以數字化集成。國內發明專利“用于增強不對稱二元調制信號的沖擊濾波方法”突破零群時延石英晶體濾波器的技術本質，用無限沖激響應（IIR）數字濾波器技術加以實現，使ABSK高效調制技術走向實用。但其濾波輸出響應往往存在較長時段的起始振蕩，這造成傳輸時間以及發射能量的浪費，對于電力線載波通信、猝發通信等要求極高傳輸效率的小數據包通信和對于能耗尤為在乎的無線傳感器網絡，不利影響非常突出。本文分析了起始振蕩產生的原因，提出了通過預先訓練的方法使沖擊濾波器直接進入穩定狀態的改進方案，無需改變濾波器的設計和結構，消除了初始振蕩，仿真結果驗證了理論分析的正確性。

　　1 不對稱的二元相移鍵控（ABSK）傳輸系統

　　ABSK調制定義如下：

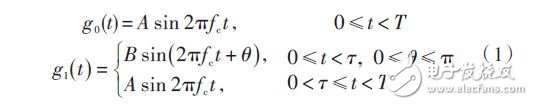
　　式中：g0 （t） 和g1（t） 分別表示碼元“0”和“1”的調制波形;碼元周期T = 2π N ωc 持續了N ? 1 個載波周期，“1”碼元的調制時間長度τ = 2πK ωc 持續了K 《 N 個載波周期，K 和N 均為整數以保證整周期調制。其中θ 和τ這兩個參數構成改變信號帶寬、傳輸碼率和解調性能的調制指標。

　　根據文獻對ABSK 調制的研究分析，ABSK 調制具有如下特點：頻帶利用率高，式（1）表明，ABSK 調制信號波形除在數據“1”的起始處有短時的相位及幅度的變化外，其余都是連續的正弦波，其能量集中在載頻fc處，頻譜利用率高;抗干擾能力強;復雜度低，可數字化實現，這是該類調制能實現產業化應用的基礎;適應面廣，調制參數θ 和調制占空比τ T 的改變，均可控制調制信號的帶寬和傳輸碼率，在同樣的發射功率下得到不同的傳輸性能，以適應不同的信道環境。

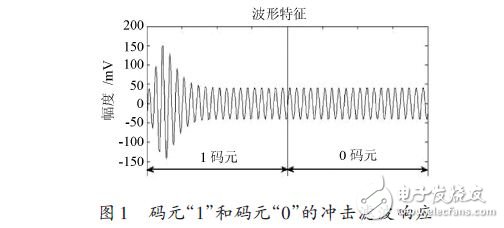
　　基于以上特點，ABSK 信號的應用越來越受到重視。目前常用于ABSK信號解調的無限沖激響應（IIR）數字濾波器，由一對共軛零點和至少兩對共軛極點構成，信號載頻高于零點頻率但低于所有極點頻率，而零點頻率與極點頻率的靠近程度，至少要達到信號載頻的10-3量級。由此，該濾波器通過其通帶中心陡峭的陷波-選頻特性，可將ABSK 調制信號在碼元“1”處的相位變化信息轉換為明顯而強烈的寄生調幅沖擊，輸出信噪比得到顯著提升，但在碼元“0”處則無相應的波形沖擊，如圖1 所示。接下來，再對濾波器輸出信號進行幅度判決、位同步等常規處理，就可以簡單實現ABSK 調制信號的解調。

　　2 基于穩態的沖擊濾波器解調方案

　　2.1 起始振蕩及其產生原因

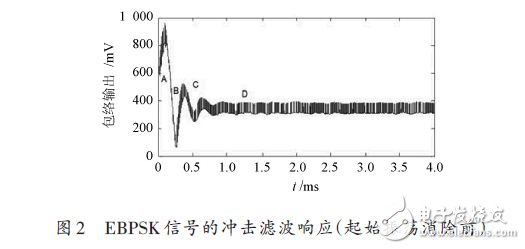
　　ABSK 調制信號的沖擊濾波響應往往存在較長時段的起始振蕩，式（1）中取fc = 10 MHz，A = B = 1，θ =π，K ∶N = 2∶40，圖2 給出了10 倍采樣頻率下的沖擊濾波器輸出響應的包絡絕對值，圖中橫坐標為時間，縱坐標為幅度。圖中AD 段為振蕩期，在這段時間內，各碼元間的沖擊幅度起伏極大，較難確定一個合適的門限以供判決。因此，實際通信中為確保可靠性常要丟棄這幾百個碼元。對于小數據包的猝發通信系統，這種傳輸時間和能量的浪費尤其不可忽視。

　　為了消除沖擊濾波器的起始振蕩，先對起始振蕩產生的原因進行分析。數字沖擊濾波器的傳遞函數為：

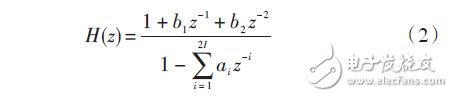
　　由于沖擊濾波器的直接2型結構比直接1型結構更簡單，這里采用直接2型結構來分析，如圖3所示。圖中的“ z-1 ”為延時單元，在硬件中可用寄存器實現。

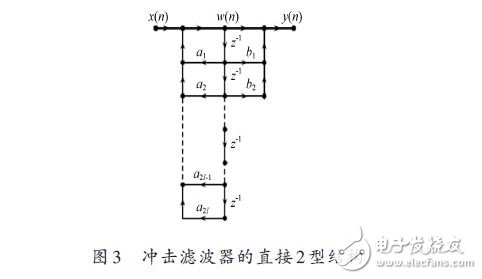
　　此時，沖擊濾波輸出為：

　　而實際通信系統必然都是因果的，因此w（ - 1），w（ - 2），w（ - 3），-，w（ - 2I） 這些值其實并不存在，習慣上將它們都取為0.隨著通信的開始，沖擊濾波器便利用實際接收到的ABSK信號進行“自我調整”，以使其狀態逐漸“步入正軌”，慢慢接近穩定濾波時所需的值，此時沖擊濾波器也逐漸進入穩態。正是這種沖擊濾波響應從無到有、濾波器狀態從初始零狀態調整至穩態的過程，形成了濾波響應起始階段的振蕩期。