基于LabVIEW的彈道解算軟件設計

摘要：針對鉛垂平面內的外彈道模型，對基于LabVIEW的彈道解算方法進行研究，提出了以四階龍格庫塔算法為核心的解算方法。使用LabVIEW編寫了彈道解算程序，在初始點狀態已知的情況下，快速高效的遞推出外彈道軌跡與落點坐標。程序能夠對數據進行處理與顯示。人機界面友好，易于操作。對于外彈道解算具有一定的應用價值。

現代導彈從出現已經過去了50多年，這50年當中導彈技術不斷發展。其中包括了伴隨著導彈而發展起來的新型學科-外彈道學，它不僅研究導彈飛行過程中質心的運動過程還研究了姿態控制學與制導理論等。外彈道學涉及到的技術范圍廣且需要各個學科相互聯系。本文研究的是鉛垂平面內，彈丸質心的運動軌跡，建立質心運動方程組，已知彈丸初始狀態利用四階龍格庫塔方法求解發射軌跡。據此編寫了LABVIEW程序實現解算過程并且將軌跡顯示出來。

1 質心運動方程

研究彈丸質心的運動過程，第一步要做基本假設;

1)整個發射至擊中目標的運動過程中，攻角為0。

2)彈丸是軸對稱的。

3)地面為平面。

4)飛行過程中重力加速度大小不變且垂直向下。

5)科氏加速度為0。

6)大氣條件為標準大氣條件，無風。

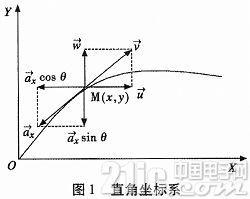
在此基礎之上，作用于彈丸的力只有重力與空氣阻力。依此彈丸的質心運動方程為式(1)。

由于ax=cHτ(y)G(vτ)v，所以得到了彈丸質心的運動方程組為式(2)。

式中：ax為空氣阻力加速度;c為具有彈丸特征的彈道系數;H(y)為空氣密度函數;G(v)為阻力函數。

2 四階龍格庫塔

四階龍格庫塔法廣泛用于模擬仿真應用中的彈道解算，在工程中被稱為“高精度單步算法”。由歐拉公式導出，k1為一階精度的歐拉公式，k2用xi點處的k1與xi+1的k2的

平均值作為平均斜率的近似值。就會得到二階的歐拉公式。以此類推得到四階龍格庫塔方程如式(3)所示。龍格庫塔法因單步四次計算，計算量大，因此廣泛使用于計算機仿真計算。

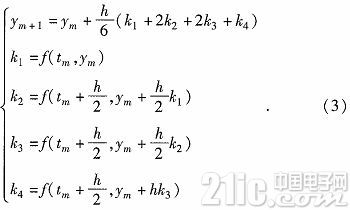
3 程序設計

根據彈丸質心運動方程組，使用四階龍格庫塔法，在LABVIEW軟件平臺編寫軟件解算彈道軌跡。在LABVIEW中依據Runge-Kutta算法VI建立解算方程。Runge-KuttaVI如圖2所示。

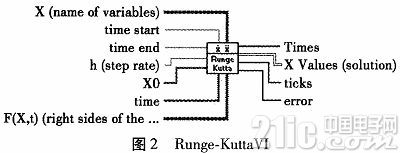
此VI需要初始狀態的數據。根據彈丸質心運動方程組，初始點已知。當t=0時，x=0;y=0;u=V0COSθ0;w=vosinθ0。θ0為發射角已知。X(name of variables)為變量名稱將質心運動方程組所涉及的變量名設置為字符串數組。time start為初始時間為0，time end為結束時間。h(steprate)為步長設置為1。X0為對應于X變量名的數據信息，這里設置u=700;w=700;y=0;x=0。time設為t。F(X，t)為對應變量名的函數名。程序設置如圖3所示。

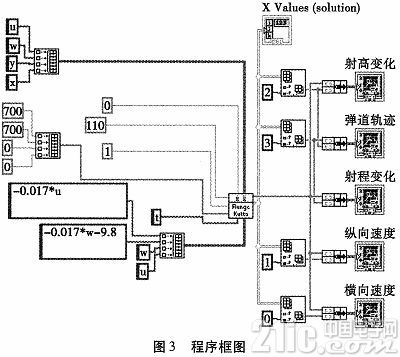
4 結論

以固定的彈體，在標準大氣壓條件下，c為常數;x，y為0;縱向與橫向初速度分別設為100、200、300、400、500。記錄解算數據：時間、最大高度、最遠距離如表1所示。

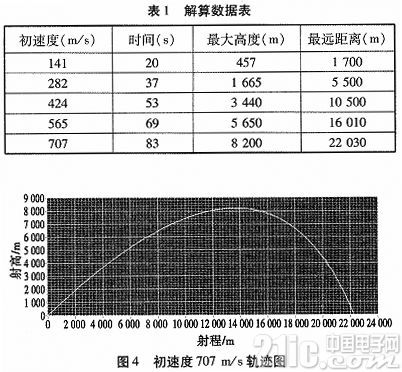
初速度為707 m/s解算出的軌跡曲線如圖4所示。

經過數據仿真實驗，得出結論。此彈道解算軟件具有可靠性，解算出的彈道數據對彈道研究具有一定的現實意義。