一種模擬濾波電路數字化方法

摘要 在信號處理中，濾波的優劣直接影響信息的準確性。模擬濾波雖然快捷但不靈活，數字濾波效果雖好但復雜。所以文中提出一種以模擬濾波器為基準，設計具有相同功能而且參數可調的數字濾波器的方法。并以二階RC無源低通濾波電路為例對此過程進行說明，與模擬濾波電路和傳統的數字濾波相比，該方法不僅比傳統的數字濾波算法簡單快捷，而且可有效防止模擬電路中器件的寄生參數、精度、溫度等的影響，使濾波更加穩定。

隨著信息科技的發展，信號處理得到了大幅推動，已經被廣泛應用于雷達、通信、自動化、航空航天等領域。在信號處理系統中，輸入信號通常含有各種噪聲和干擾。為對信號進行準確的測量和控制，必須削弱或濾除被測信號中的噪聲和干擾。一般在系統中可選用硬件濾波和軟件濾波。硬件濾波又分為無源濾波和有源濾波，無源濾波是通過RC濾波器或LC濾波器等模擬濾波器進行濾波。軟件濾波也稱數字濾波，是通過一定的算法削弱噪聲的影響。硬件濾波的優勢是不需要進行復雜的程序處理，反應靈敏。而軟件濾波的優勢是不需要硬件的投入，而且可靠穩定。

綜合兩者的優勢，本文提出了一種以低通二階RC無源濾波電路為基準，用Matlab和Visual C++設計一個具有相同功能數字濾波器的方法即模擬電路數字化方法，以濾除信號中的高頻雜波，得到了較為理想的波形。

1 模擬電路數字化方法

模擬電路數字化的過程如下，首先從硬件濾波電路出發，計算電路的傳遞函數H(s)。由于軟件濾波的信號是離散的數字信號，所以將H(s)轉換成離散域的H(z)，通過Matlab編程實現對信號的濾波。如果濾波效果不理想，則對傳遞函數中的參數進行調整，得到具有較理想濾波效果的H(z)。為最終用Visual C++編程實現，需要將H(z)反變換得時域的h(t)，與信號進行卷積和運算以完成濾波。經過以上步驟，完成模擬濾波電路數字化的過程，并在Matlab和Visual C++平臺上實現濾波。

2 二階RC無源低通濾波電路

對于模擬電路的分析，通常采用傳遞函數的分析方法。電子電路往往是由若干個動態環節連在一起構成一個復雜電路。對于每個具體環節來說，都有它的輸入量和輸出量，而一定輸入量的變化都會引起輸出量的變化。根據一個環節中所進行的物理過程可以寫出微分方程，它表示了該環節輸出量和輸入量的關系。

例如RLC振蕩回路的微分方程為

輸入量與輸出量都是時間t的函數，用微分方程直接表示輸入量與輸出量時間函數之間的關系比較復雜。但利用拉氏變換把時間函數變換為s的函數以后，原函數對于時間t的微分積分就簡化為s的乘除法。

在零起始條件下，一個動態環節的輸出量的拉氏變換用X(s)表示，輸入量的拉氏變換用F(s)表示，把

稱為傳遞函數。

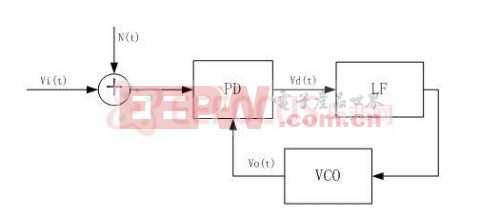
通常信號在進行放大之前，先對該信號進行濾波。以低頻信號為例，使用經典的二階RC無源濾波電路進行濾波，電路如圖1所示。在接下來的部分將以此電路為例對模擬電路數字化方法進行詳細的分析和講解。

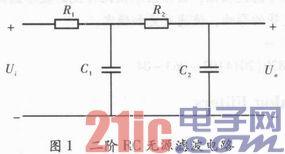
計算出該電路的傳遞函數H(s)如式(2)所示。其中，b=R1C1+R1C2+R2C2，a=R1R2C1C2。

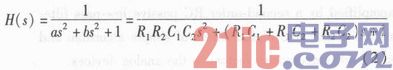
3 傳遞函數離散化

濾波器的濾波效果與R1、R2、C1和C2等參數相關，如果取值不當會造成濾波效果不理想。對于復雜的傳遞函數，諧振頻率和帶寬不易計算，所以本文采用控制變量法。

對于多因素的問題，常常采用控制因素的方法，把多因素的問題變成多個單因素的問題。每一次只改變其中的某一個因素，而控制其余幾個因素不變，從而研究被改變的這個因素對事物的影響，分別加以研究，最后再綜合解決，這種方法叫控制變量法，被廣泛地運用在各種科學研究之中。

得到傳遞函數后，就可以對信號進行濾波。由于待處理的數據是數字信號，若想仿真需將頻域的傳遞函數轉換為x域的傳遞函數，即將模擬濾波器轉換為數字濾波器。模擬濾波器轉換為數字濾波器有兩種方法：脈沖響應不變法和雙線性變換法。

脈沖響應不變法是一個穩定的設計，主要用于設計某些要求在時域上能模仿模擬濾波器功能的數字濾波器。這種變換法的主要特點是頻率坐標的變換是線性的，即由于混疊現象，阻帶邊緣的衰減要比模擬濾波器稍差一些，但仍能滿足技術指標的要求。脈沖響應不變法要求該模擬濾波器是帶通濾波器或者低通濾波器，但這種方法在阻帶沒有起伏的情況下才有用。

雙線性變換法映射也是一種穩定的設計，不存在混疊現象，對能夠變換的濾波器類型沒有限制。但這種方法也有固有缺陷：模擬頻率和數字頻率之間是非線性關系，它使得頻率的標度彎曲，不能保持原來的模擬濾波器的相頻特性;數字的頻率響應與模擬的頻率響應有明顯的差別。一般情況下，可以通過頻率的預畸變進行校正。但總體來說，雙線性變換法的仿真結果比脈沖響應不變法更加理想。

由于脈沖響應不變法從s平面到z平面是多值映射，會在頻域響應產生混疊失真。而雙線性變換法可以把整個s平面變換到整個z平面上去，且使s的左半平面映射到z平面的單位圓內，所以設計采用雙線性變換法。

雙線性變化法的映射函數為

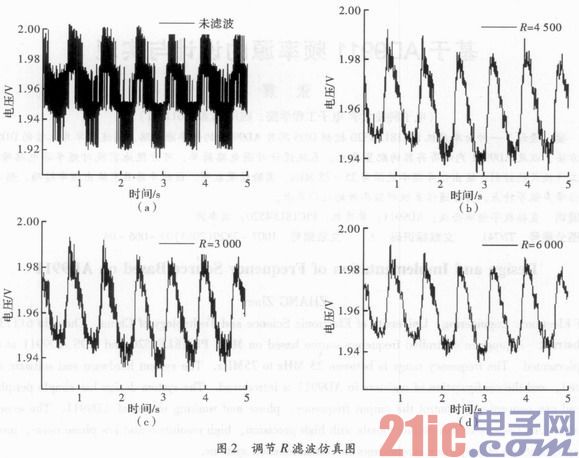
調用Matlab中的Fiher函數R1和R2調節參數、進行仿真，仿真結果如圖2所示。圖2(a)是未加濾波的波形，圖2(b)、圖2(c)、圖2(d)的電阻依次增大，從圖中可以看到，電阻越大，高頻分量越少。

4 時域傳遞函數

Matlab一般只用于功能仿真，而實際項目應用，通常采用Visual C++軟件編程進行信號控制和硬件實現，所以需要將Matlab仿真時使用的濾波器函數Filter轉化為C代碼實現。

軟件編程有時域和頻域兩種思路。由于輸入信號較為復雜不易進行時-頻轉換，只能采用時域濾波。所以需將傳遞函數反變換到時域，對信號進行濾波處理。

5 時域卷積濾波

卷積在通信技術和信號處理中起著重要的作用。在線性時域系統中，根據時間的連續性，可以分為卷積積分和卷積和。在LTI連續時間系統中，把激勵信號分解為一系列沖激函數，求出各種沖激函數單獨作用于系統時的沖激響應，然后將這些響應相加就得到系統對于該激勵信號的零狀態響應。這個相加的過程表現為求卷積積分。在LTI離散系統中，可用上述方法進行分析。由于離散信號本身是一個序列，因此，激勵信號分解為單位序列的工作就較容易完成。如果系統的單位序列響應為已知，那么，也不難求得每個單位序列單獨作用于系統的響應。把這些序列相加就得到系統對于該激勵信號的零狀態響應，這個相加的過程表現為求卷積和。

由于本系統中的信號是離散時間序列，常用的卷積和的求解方法有圖解法、對位相乘求和法、解析法和列表法等4種。一般，待處理的信號的數據量比較大，列表法不適用，所以采用解析法。

卷積與傅里葉變換有著密切的關系。利用兩個函數的傅里葉變換的乘積等于它們卷積后的傅里葉變換的性質，能使傅里葉分析中許多問題的處理得到簡化。本文正是采用這一點，將頻域的濾波轉化為時域濾波。

頻域相乘等效于時域卷積。編寫C程序求輸入信號和傳遞函數的卷積和。當兩個信號為因果信號時，可以根據式(5)求卷積和。當f1(k)的數據長度為m;f2(k)的數據長度為n(n

6 結果及分析

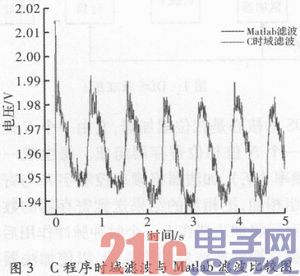
信號分別經卷積和濾波和Filter函數濾波，將濾波后的數據導入Matlab比較，結果如圖3所示。由圖可見，前者在初始狀態出現尖峰，這是因為卷積和是在特定窗口內時域累加的過程，會造成頭部數據和尾部數據不準確。雖然編寫的C卷積和濾波程序有一定的缺陷，但是整體波形一致，說明實驗獲得初步成功。

7 結束語

提出了一種將硬件濾波電路數字化的方法，并在Matlab和Visual C++平臺上得以實現。與模擬濾波電路和傳統的數字濾波相比，不僅比傳統的數字濾波算法簡單快捷，而且有效防止了模擬電路中器件的寄生參數、精度、溫度等的影響，使濾波更加穩定。