運用齊次性定理分析理想運算放大器

　　根據(jù)理想運算放大器線性應(yīng)用的特點,運算電路的傳統(tǒng)分析方法是采用"虛短"和"虛斷"的概念分析輸出與輸入的運算關(guān)系。在電路理論中運用齊次性定理分析線性網(wǎng)絡(luò)十分方便。為了簡化理想運算電路的分析方法,運用齊次性定理,采用"倒推法"分析了幾種常用的運算電路的輸出與輸入的運算關(guān)系,得出了與傳統(tǒng)分析方法同樣的結(jié)果。結(jié)果表明,用該定理分析理想運算放大器簡單方便、快速準(zhǔn)確。

　　l 齊次性定理

　　定理 在線性電路中，當(dāng)所有獨立源都增大或縮小K倍時(K為實常數(shù))，各支路電流或電壓也將同樣增大或縮小K倍。

　　定理應(yīng)用方法：先假設(shè)運算放大器輸出量uo為1，倒推出信號源電壓u1在假設(shè)條件下的取值為uIj，則由齊次性定理可得出輸出量的實際值：

　　2 基本運算電路的分析

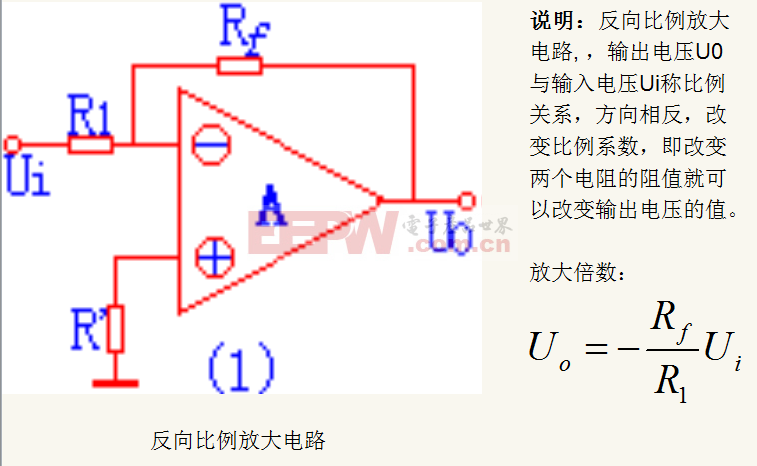
　　2.1 反相比例運算電路

　　反相比例運算電路如圖1所示。

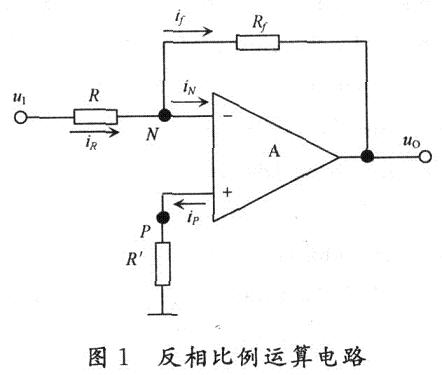
　　假設(shè)uo=l，根據(jù)“虛斷”和“虛地”有：

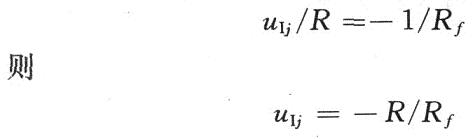
　　根據(jù)齊次性定理：

　　2.2 同相比例運算電路

　　同相比例運算電路如圖2所示。

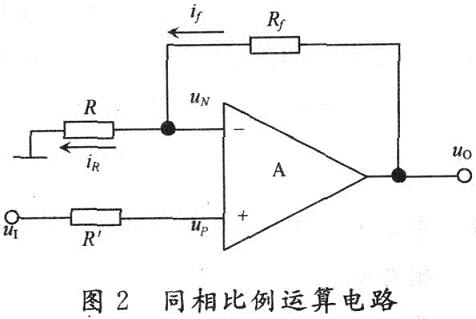
　　假設(shè)uo=1，根據(jù)“虛斷”和“虛短”有：

　　2.3 積分與微分運算電路

　　對積分與微分運算電路，由于輸出電壓等于輸入電壓的積分或微分(不存在線性關(guān)系)，齊次性定理不再適用。但若求在正弦激勵下的穩(wěn)態(tài)響應(yīng)，仍可以應(yīng)用齊次性定理。

　　2.3.1 積分運算電路

　　積分運算電路如圖3所示。

　　假設(shè)Uo=1，根據(jù)“虛斷”和“虛地”有：

　　2.3.2 微分運算電路

　　微分運算電路如圖4所示。

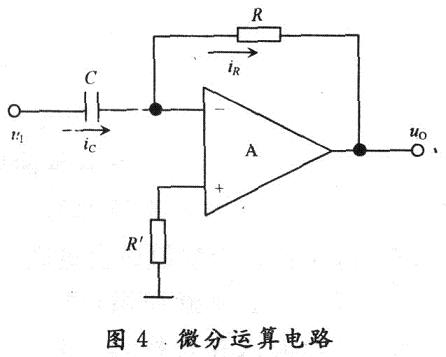
　　假設(shè)Uo=1，根據(jù)“虛斷”和“虛地”有：

　　3 復(fù)雜運算電路的分析

　　[例]電路如圖5所示。試寫出輸出電壓uo的表達(dá)式。

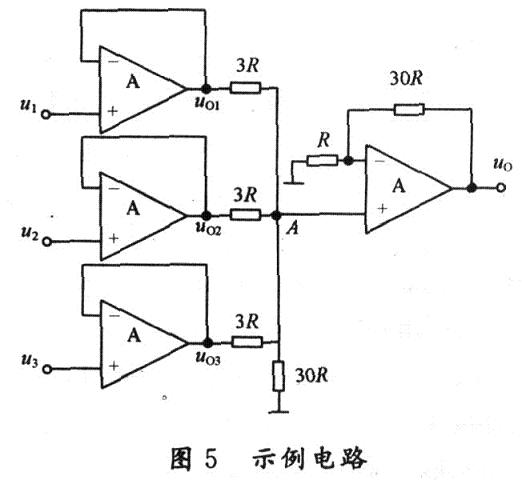
　　假設(shè)uo=1，根據(jù)“虛斷”和“虛短”有：