基于一種非等距線陣的寬帶信號處理方法
摘要:獲得寬帶信號的波達方向,提出一種基于非等距的參差線陣方法。利用孫子定理、解模糊條件、分頻帶相控陣等方法解釋非等距線陣。構造出的參差線陣通過處理合成,保持陣列對不同頻率指向的一致性,達到信號功率非相參積累的預期效果。解模糊得到信號的波達方向,通過實驗仿真驗證方法可行。
關鍵詞:非等距線陣;寬帶信號;解模糊;FFT
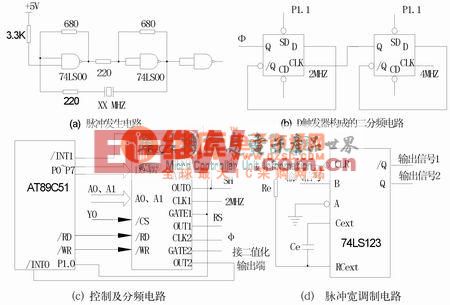
目標雷達信號可能是寬帶信號,系統波段可能進一步擴展。由于饋源尺寸不能無限度地縮小,系統帶寬、饋源尺寸、饋源間距將成為相互矛盾的需求,為了解決這個困難,擬在陣面左右兩側采用非等距間距,比如在右側采用3/2波長間距,而左側采用4/2波長的間距,利用間距的3與4互質的關系,可進行角度解模糊,獲得真實的信號到達角。
1 非等距間距解模糊條件證明
利用測量所得陣元間的相位差φi(θ),可根據孫子定理惟一確定無模糊信號DOA。
孫子定理基本原理:

b1,b2,…,bs為余數,當m1,m2,…,ms為兩兩互質的整數時,對任意的整數b1,b2,…,bs,總有整數解x,且此解在模m=m1,m2,…,ms意義下惟一。其解可通過如下方法求得。
記Mi=m/mi,先求ui使:
uiMi≡1 mod(mi) 1≤i≤s
則有:
u1M1+u2M2+…+usMs≡1 mod(m)
令ei=uiMi,i=1,2,…,s,則孫子方程式的解為:
x≡b1e1+b2e2+…+bses mod(m)
利用孫子定理解DOA模糊的基本思路是:
選擇兩兩互質的陣元間距di(與定理中的mi對應),根據測量所得的陣元間相位差φi(θ)(與定理中的bi對應),則可利用孫子定理惟一確定無模糊DOA(與定理中的x對應)。
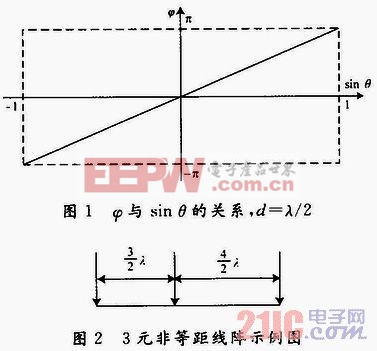
因為兩陣元間相位差φ(θ)=2 πdi/λsinθ,在無模糊測相條件下,d=λ/2,因此φ(θ)=πsinθ。式中,測量值φ在-π~π變化,sinθ從-1~1變化,結果如圖1所示。φ對sinθ是一條直線,具有一一對應關系,不產生角度模糊。




評論