基于頻域濾波數字均衡器的設計
加入技術交流群
2．2．2 蝶形運算的算法
蝶形運算是逐級運算累加實現的，在傳統的蝶形運算中，旋轉因子
的N是保持一個固定的值而k是不斷變化的，第一級到第
級中，k的變化是以2為底的冪指數的變化，而到第
級時，k的變化則是0，1，…，(N／2)-1。如果依照k的這種變化規律，在第級時，就很難繼續依照前級進行變化。因此，根據以上分析，采用另外一種思路來對蝶形運算進行重新的整理。在旋轉因子中，N是每個蝶形單元輸入數據的個數，k的變化規律是0，1，…，(N／2)-1，采用這種方法就可以有效的縮短代碼的長度，提高運行速度。圖1為蝶形運算流程圖。本文引用地址：http://www.104case.com/article/187578.htm
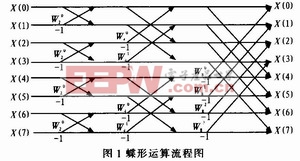
2．3 快速傅里葉變換的實現
蝶形運算的旋轉因子
，輸入的復數表示為InputData=RealInData+j*ImagInData，因此在計算過程中，旋轉因子和輸入數據的計算過程是將實數和復數分開計算所得到的。
因為旋轉因子中k=0，1，…，(N／2)-1，因此隨著k的增長cos(-2Pik／N)和sin(-2Pik／N)也相繼發生成倍的變化。
對這一現象采用的處理方法是使用正余弦的倍角公式：
這樣，處理的變化的過程就變為處理正弦和余弦倍角變化的過程，從而簡化了程序。部分程序如下：
其中，Block是每一個蝶形單元輸入個數的一半即N／2，r0和i0分別是旋轉因子的實部和虛部。
評論