諧振技術及其應用

摘要：首先介紹了硬開關電路的缺陷，引出諧振技術，然后詳細分析了基本電路在不同的初始條件下的工作情況，接著分析了諧振參數間的關系及其會帶來的問題。最后，介紹了該技術的應用，同時分析該技術在變換器中存在的問題。

關鍵詞：硬開關；軟開關；諧振技術

Resonant Technique and Its Application

SUN Ze, WANG Gang

Abstract:The faults of hard switching circuit are first analyzed, then the resonant technique by using a basic circuit is introduced and the relation between the resonant parameters and questions produced possibly are analyzed. At last, its application and existing questions in converter are presented.

Keywords:Hard switching; Soft switching; Resonant technique

中圖分類號：TN86文獻標識碼：B文章編號：0219－2713(2002)3－0093－04

1 引言

在開關電源中，通常采用磁性元件（如鐵心電感、變壓器等）實現交流/直流側的濾波，能量存儲和傳輸。這些磁性元件在電源裝置的體積、重量、成本中占有很大比重。開關器件的工作頻率越高，磁性元件的尺寸就可以越小，電源裝置的小型化、輕量化、低成本化就越容易實現。但是，傳統的PWM變換器中的開關器件工作在硬開關狀態，存在很多缺陷：

1）開通和關斷損耗大；

2）感性關斷問題；

3）容性開通問題；

4）二極管反向恢復問題。

由于硬開關工作時存在上述四大缺陷，所以使開關器件工作頻率的提高受到限制，從而電源裝置的小型化、輕量化、低成本化也就不易實現。克服以上缺陷的有效辦法就是應用軟開關（SoftSwitching，簡稱SS）技術。最理想的軟開通過程是：電壓先下降到零后，電流再緩慢上升到通態值，所以導通損耗近似為零。另外，因器件導通前電壓已下降到零，器件結電容上的電壓亦為零，因而解決了容性開通問題，這意味著二極管已經截止，其反向恢復過程結束，因此二極管反向恢復問題亦不復存在。最理想的軟關斷過程是：電流先下降到零，電壓再緩慢上升到斷態值，所以關斷損耗近似為零。由于器件關斷前電流已下降到零，即線路電感中電流亦為零，所以感性關斷問題得以解決。事實上，這兩個過程要么存在感性關斷問題，要么存在容性開通問題。也就是說，僅僅利用一個電感或電容是不能根本解決問題的，所以最好的情況應當是使開關在電壓和電流同時為零時關斷和開通，損耗才會真正為零。而要實現這個目標，就要用到諧振技術。

2 諧振技術

2.1 諧振過程

根據電路原理，電感電容串聯或并聯可構成諧振電路，使得在電源為直流電源時，電路中的電流按正弦規律變化。由于電流或電壓按正弦規律變化，存在過零點，如果我們能夠在這一時刻開通或關斷，產生的損耗就為零。下面就分析電源里用得最多的二次串聯諧振電路，對其在初始情況不同時的工作情況進行討論。基本電路如圖1所示。

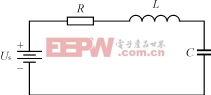
圖1 基 本 二 次 串 聯 諧 振 電 路

假定電容C上的電壓為uC，電感L中的電流為iL，電源電壓為Us。于是，該電路的微分方程為：

L(di/dt)＋Ri＋uc=Us （1）

i=C(duc/dt) （2）

將式（2）代入式（1），得

LC(d2uc2/dt2)＋RC(duc/dt)＋uc=Us （3）

式（3）對應的齊次方程為：

LC(d2uc2/dt2)＋RC(duc/dt)＋uc=0 （4）

該齊次方程對應的特征方程為：

LCs2＋RCs＋1=0 （5）

在R條件下，求得方程的解為：

s1=－β＋jω′

s2=－β－jω′ （6）

式中：β=R/2L；

ω′=；

ω0=。

于是，式（4）的解為：

=e－βt(A1cosω′t＋A2sinω′t) （7）

很顯然，uc=Us是方程的一個特解，即

=Us （8）

可得，式（3）的通解為：

uc=y=＋

=e－βt(A1cosω't＋A2sinω't)＋Us （9）

下面分別討論該電路在不同初始條件下的解以及相應的電壓電流波形：

1）第一種情況

初始條件為：iL=0，uc=0。方程的解為：

uc=－e－βtsin(ω't＋ arctan)＋Us (10)

iL=e－ βtsin(ω't) （11）

波形如圖2所示。

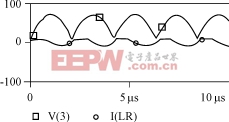
圖2 初 始 條 件iL=0，uc=0時uc，iL波 形