開關電源滑動模型圖形分析方法

1　引　言

開關電源通常有兩大研究領域，一個是拓撲結構領域的研究，即開關電源的電路結構研究;另一個是控制方法領域的研究，一個控制方案的好壞往往決定開關電源的性能，實際工程中控制方案的復雜程度決定電源的造價的高低，因此很多電源設計者在控制方法的設計上投入了很多關注，并提出了各種控制方法。應用于開關電源的控制方法通常分為兩大類：一類是線性控制方法，另一類是非線性控制方法。常用的電壓閉環控制、電流閉環控制、雙環控制和函數控制均屬于線性控制方式。近期發展單周期控制、前饋控制、自適應控制和滑模控制則屬于后者。在各種控制方案中，由于滑模控制對系統攝動和外界干擾在一定條件下具有不變性，即很強魯棒性，所以得到研究者越來越多的關注。如文獻[1]在開關變換器中應用滑模控制作了一定的研究。文獻[2]則提出了Buck-Boost型AC-DC變換器的滑模控制的解決方案。以上文章雖然都導出控制模型并選取了參數，但未對參數是否滿足滑模運動的條件給出證明。文獻[1]中還曾提到不能單獨采用電壓誤差作為直接控制對象，同樣也未對不能單獨采用電壓誤差作為直接控制對象的原因作詳細證明。而在滑模控制中，參數的選擇是非常重要的，它決定了系統工作的性能，不恰當的參數選擇有可能導致滑模運動不能形成或者是不穩定。文獻[3]雖然給出了傳統的證明方法，但是該方法并不是很直觀，而且比較復雜。本文則將通過有別于傳統方法的方法給出保證系統穩定的參數選擇證明。

2　滑模控制

滑模控制是在對繼電系統的研究中發展起來的，是一種特殊的變結構控制。其特殊性在于該控制有切換，而且在切換面上系統將會沿著固定的軌跡產生滑動運動。要實現滑模控制，就要做三項工作：切換面的選取，控制函數的求取，參數的確定。其中參數的選擇必須滿足文獻[3]中指出的滑模控制的三個要素：進入條件、存在條件和穩定條件。進入條件是保證系統對任意初始位置，運動都能夠到達切換面。存在條件是保證這種運動到達切換面后，能在切換面上產生滑動運動。穩定條件有兩個方面，一個是滑動的穩定條件，一個是系統的穩定條件。而這里的穩定條件則指的是系統在切換面上的滑動運動能夠向工作點運動。當參數確定后，切換面和控制函數也隨之確定。所以滑模控制問題最終轉化為求取這三個要素的問題。三個要素的傳統確定方法在文獻[3]中作了詳細的描述，但文獻[3]中的三要素確定方法并不直觀，計算起來也比較復雜，本文將針對這種情況提出一種利用圖形確定滑模控制三要素的方法。同時，通過圖形直觀的說明切換面的不同選擇對于系統性能的影響。

3　Boost電路的建模

Boost變換器的一般原理圖如圖1所示

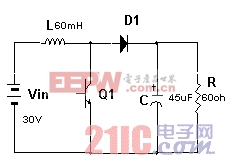
圖1　Boost變換器原理圖

以輸出電壓 和電感電流 作為狀態變量。T表示開關的開關狀態，T=1表示開關開通，T=0表示開關關斷。當T=1時，其狀態方程為：

(1)

當T=0時，其狀態方程為

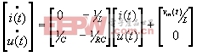
(2)

兩者合并為

(3)

穩態時,

,代入方程(3)可求出穩態電壓，電流為

(4)

以誤差

，

作為變量，分別代入到(1)，(2)中

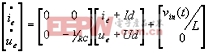
(5)

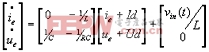
(6)

4　相平面圖

利用計算機(本文采用MATLAB)分別作出式(5)和(6)的相平面圖，設定電源為恒定值30伏，輸出電壓設定為60伏，L=60mH,C=45μF,R=60Ω。

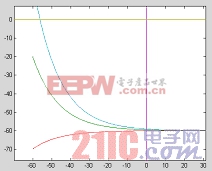
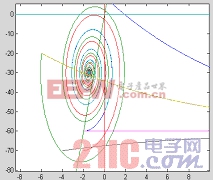
圖2　T=1時系統運動相平面圖　　圖3　T=0時的相平面圖(環狀曲線)

圖2是由方程(5)確定的，對實際電路進行定性分析可知，當開關閉合后，由于無能量從電源端向輸出端傳遞，達到穩定時，輸出電壓漸變為零，那么誤差就穩定在-60伏。電源經過電感放電，電流是線性增大的，因此電流誤差先減少后增大。這與仿真結果相同。圖3將兩種狀態的相平面畫在一起，其中逆時針旋轉曲線由方程(6)確定，分析實際電路可知，輸出電壓最后穩定于30伏，即與輸入電壓相同，那么誤差穩定于-30，仿真結果與分析結果相同。

5　三要素分析及試驗仿真

下面我們通過相平面各個區域的運動特性來分析滑模控制的三要素，并通過不同參數的選擇來分析參數對系統性能的影響。

從圖1我們可以看出，在實際電路中，輸出電壓不可能等于負值，因此只有電壓誤差大于等于-60伏的空間對于我們的研究才有意義。

由于開關的頻率不可能為無窮大，同時控制電路本身所具有的延時性，從而容易產生抖動，這也是制約滑模控制發展的主要因素。本系統為了減少抖動，采用指數趨近率

切換面為

下面我們通過不同的

的選擇來對系統進行分析。

5.1 切換面為

切換面為

，即取橫軸作為滑模面，相平面，運動軌跡分別如圖4，圖5所示。我們從圖3中可以看出，要使系統運動能夠進入切換面，運動起點必須在起始于點(-2，-70)的曲線所包圍的區域之外。因此在這種情況下要滿足進入條件比較困難，如開始于(-2,-60)的運動就不能到達該切換面，而且在負半軸上不存在產生穩定的滑動運動的條件，這就說明了文[1]中為什么不能單獨采用電壓作為直接控制量。

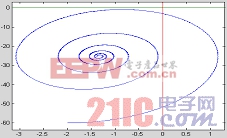
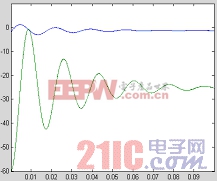
圖4　 的相軌跡　　　　圖5　 的系統運動軌跡(幅度大的是電壓，幅度小的是電流，以下相同)

5.2　切換面為

切換面為

，即取豎軸為切換面，相平面，運動軌跡分別如圖6，圖7所示。從圖3中很容易看出來該切換面滿足前面三個條件,由于只采用了一個狀態變量，在實際電路搭建時，整個控制設計得以簡化!

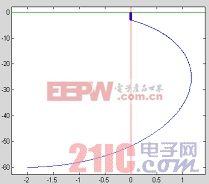
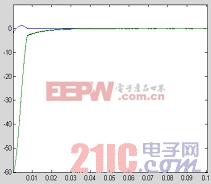
圖 6　　的相軌跡　　　　　　　　　　 圖 7　　的系統運動軌跡

5.3

接下來分析切換面在一，三相的情況：如圖3，開始于(-2，-60)即初始狀態的運動軌跡有兩個，一個是當T=1時系統的運動軌跡(直線)，另一個是T=0時系統的運動軌跡(逆時針曲線)。要讓系統運動進入滑動面

并產生滑模運動,就要使

-30(30為通過原點和(-2，-60)兩點直線的斜率)，雖然當斜率在26-30之間同樣滿足穩定要求，但整個系統抗干擾能力比較差。

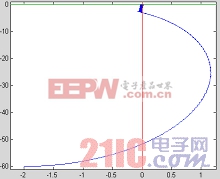
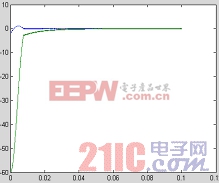
圖8　相軌跡　　　　　　　　　　圖9　系統運動軌跡

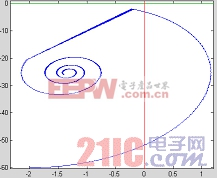
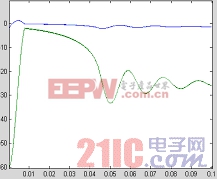
圖10　相軌跡　　　　　　　 圖11　　系統運動軌跡

5.4

當切換面位于二，四相限時，在電壓誤差等于-60伏以上空間，T=1,T=0時系統的運動軌跡在同一過程中都有兩次經過切換面，一個是遠離切換面，另一個是進入切換面。由文獻[3]可知，雖然系統有機會進入切換面，但在切換面上不可能產生滑動運動，所以不適宜在此區域選擇切換面。

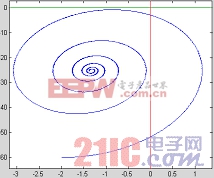
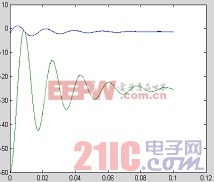
仿真結果完全與分析一致。該方法借助計算機，沒有復雜的公式推導，而且比較直觀，從而證明該方法正確性和簡單性。

6　結 論

本文通過圖形法分析開關電源的滑動模型，確定了保證系統穩定的參數的選擇范圍以及分析了運動特性變化的特點。從仿真結果上證明該方法比傳統分析方法簡單、直觀。但由于作圖的維數限制，應此該方法只能應用于三階及三階以下系統。而開關電源有很大一部分是二階，三階系統，比如說Boost,Buck,正激變換器，反激變換器等都是二階系統，因此該方法的提出對于滑模控制在開關電源中的研究是很有意義的!

參考文獻

1.周宇飛等，Boost變換器滑模控制方法及其實驗研究，電力電子技術[J]2000.1.4:42-44

2.朱長海等，基于滑模控制的Buck-Boost型AC-DC變換器,洛陽工學院學報[J]2002.23(1):85-88

3.姚瓊薈，黃繼起，吳漢松，變結構控制系統，四川：重慶大學出版社，1997：14-52