基于ATmegal28的LED屏圖像數(shù)據(jù)解碼設計

2．1 Huffman解碼的實現(xiàn)
Huffman解碼是解碼過程中重要的一環(huán)。傳統(tǒng)的哈夫曼解碼需要逐位查找哈夫曼表，進行比較判斷，由于查找過程需要大量的移位及循環(huán)。這樣的解碼效率非常低。針對這種情況，充分考慮到ATmegal28的存儲容量的限制，在讀文件頭時，軟件事先構造出不同碼長下的哈夫曼碼字的最小值表和最大值表如表1所示，最小值在哈夫曼表中的索引以及哈夫曼樹各葉子結(jié)點對應的編碼表。

在解碼的時候，讀取1串二進制數(shù)據(jù)，分別與各碼長下的最大值和最小值進行比較，如果在哈夫曼表中沒有該碼長的碼字，說明該比特數(shù)據(jù)不是完整的Huff_man編碼，接著讀取下一個比特數(shù)據(jù)加在前面的比特數(shù)據(jù)組成的新的碼字，然后再在最小值表和最大值表中進行查找，直至找到確切的碼字。最后把該碼字減去同一碼長下最小值，加上此最小值在哈夫曼表中的索引即可得到該碼字在編碼表中的位置。
2．2 IDCT變換的實現(xiàn)
將8×8塊中的顏色分量單元的64個值逐一乘以對應的量化表內(nèi)位置相同的系數(shù)，然后再將64個數(shù)據(jù)進行Z字型的重新排列，進行IDCT變換。IDCT的運算量很大，其中要進行大量的浮點乘法和加法運算，因而在解碼過程中IDCT所占時間最多。采用行列分解法先將二維IDCT分解成一維8點的IDCT，對于一維8點IDCT采用Loeffler的快速算法。圖2為Loef―fler算法的流程圖，Loeffler算法運算因子的解釋如圖3 所示。

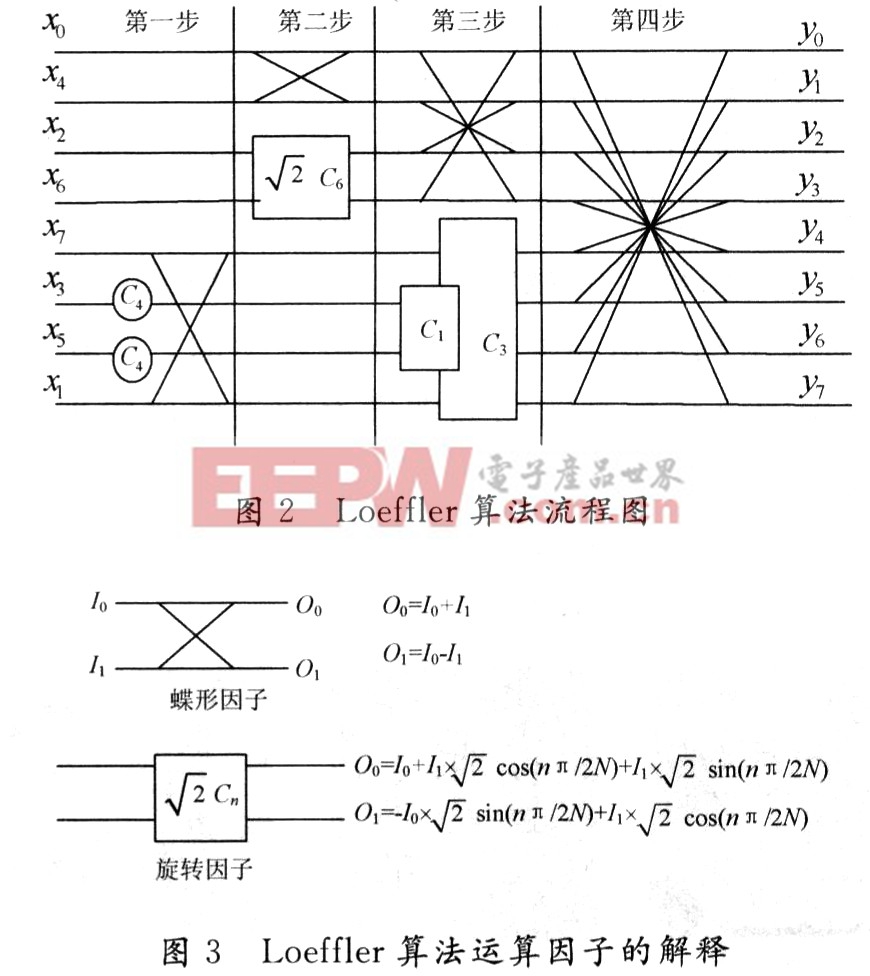
直接對旋轉(zhuǎn)因子進行計算需要4次乘法和2次加法，這樣1次8個點的一維IDCT變換總共需要14次乘法和26次加法。可以對旋轉(zhuǎn)因子進行變形如式(1)所示：

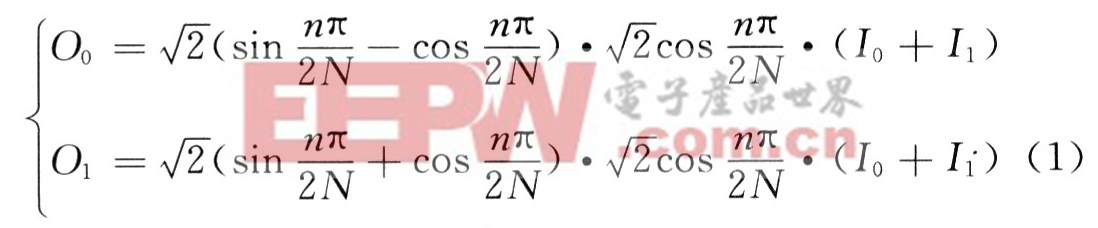
從而1次旋轉(zhuǎn)因子計算只需要3次乘和3次加。進而進行1次一維IDCT只需11次乘和29次加。因為乘法運算的代價高于加法運算，所以這種變形是有益的。完成一次二維的IDCT運算總共要進行16次的8點一維IDCT運算。由于ATmegal28在速度方面的限制，在IDCT運算過程中把浮點操作改進為整形運算，并且把的值擴大211倍存儲起來，為IDCT運算做準備。