二級倒立擺的模糊控制研究
加入技術交流群
在倒立擺系統中，Q，R分別用來對狀態向量x和輸入控制量u進行平衡加權。一般情況下，P增加時，控制力減小，角度變化變小，跟隨速度變慢。而Q中某元素增加時，其對應的狀態變量的響應速度也增加，其他狀態變量的響應速度相對減慢。為了使得反饋矩陣K更合理，對矩陣Q，R的選取一定要盡量恰當。通過反復測試，實際系統的控制過程選取Q=diag[500 700 700 0 0 0]，R=1。
根據二級倒立擺的參數，基于MATLAB強大的矩陣運算及其豐富的內部函數，利用K=lqr(A，B，Q，R)命令計算，可得到狀態反饋矩陣K：
本文引用地址：http://www.104case.com/article/163392.htm 
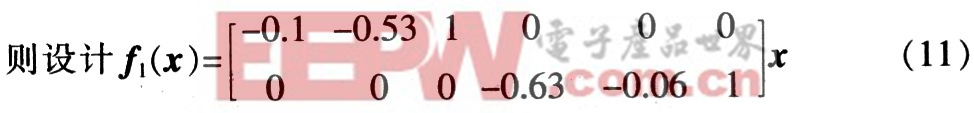
從而得到綜合誤差E和綜合誤差變化率EC。
3．2 降維后設計二維Mamdani型模糊控制器
輸入變量E、EC，輸出變量u；E、EC論域設定：E=[-6，6]，EC=[-6，6]，輸出論域U=[-1，1]均采用三角型、全交迭、均勻分布隸屬度函數。每個變量用5個模糊子集{NB NS ZE PS PB}來描述，隸屬度函數曲線圖如圖2、圖3所示。EC的隸屬度函數曲線同E的隸屬度函數曲線。
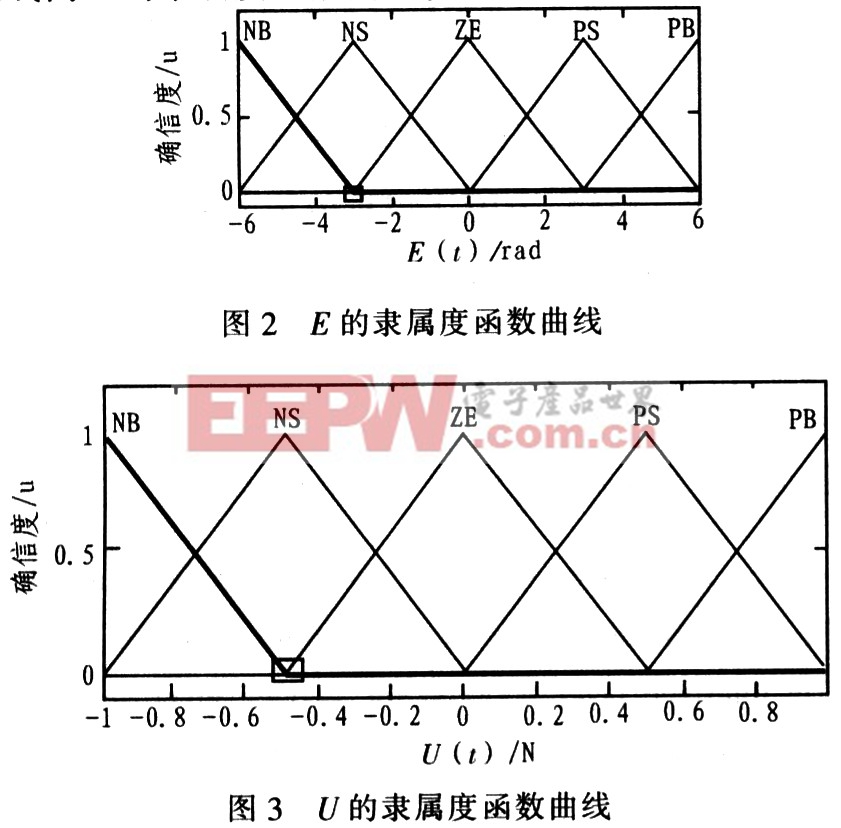
模糊推理采用Mamdani最小運算規則。根據輸入、輸出論域上的模糊語言變量劃分NB(負大)，NS(負小)，ZE(零)，PS(正小)，PB(正大)，設計模糊推理規則如圖4所示。
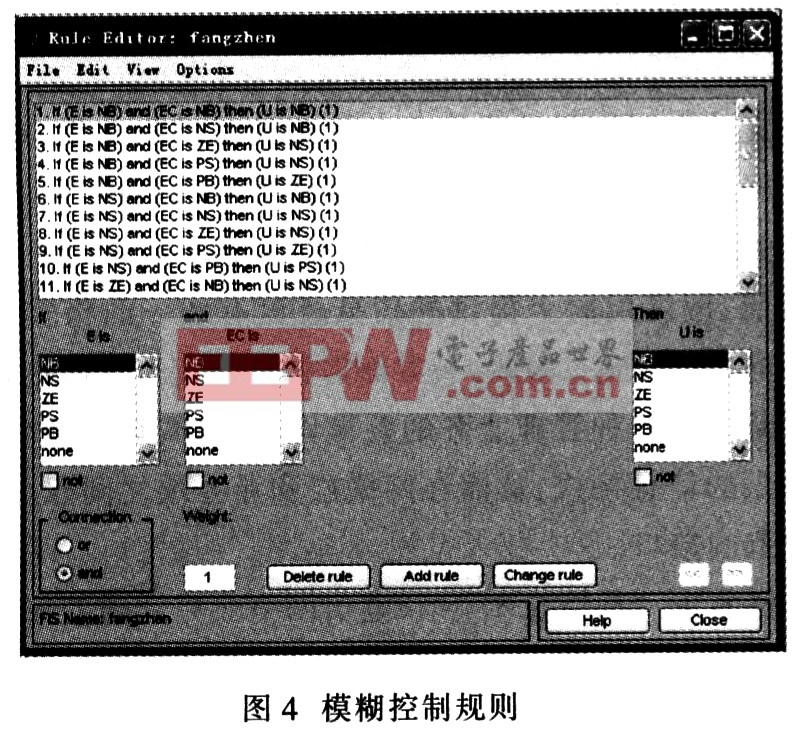
模糊控制器采用重心法實現非模糊化，與一般采用的最大隸屬度法相比較，重心法具有更加平滑的輸出推理控制。通過以上分析和試驗，并恰當地選擇模糊邏輯系統的參數，從而設計一個適合被控對象的模糊控制器，如圖5所示。圖5中，Ke、Kec為量化因子，Ku為比例因子，State-Space為系統的狀態空間方程，Saturation為限幅模塊，Scope為示波器模塊。根據以上工作，在Simulink環境中對二級倒立擺系統進行仿真，其仿真曲線如圖6所示。
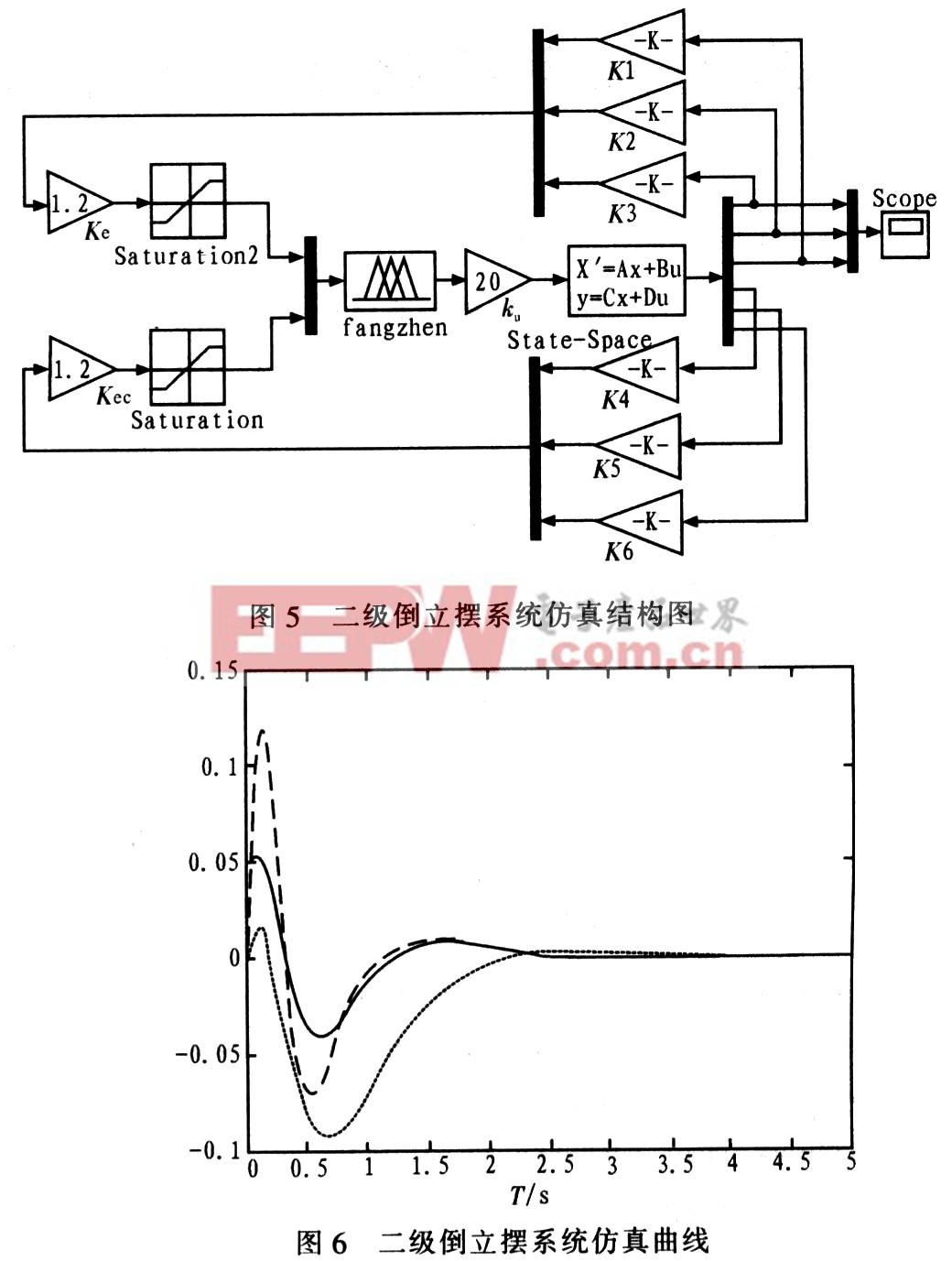
4 結束語
二級倒立擺是典型的多輸入、非線性、強耦合系統。通過設計融合函數降低控制器的輸入維數，用模糊控制解決多輸入系統時遇到的模糊規則爆炸問題，使設計的實用模糊控制器成為可能。融合函數的設計方法還可推廣應用到一級、三級倒立擺系統中。該模糊控制器設計切實可行，能較好地控制系統，達到較好的控制效果。模糊控制具有魯棒性和穩定性好、算法簡單等特點，應用在實時性要求較高的場合，該控制方法也可應用到其他多變量、非線性系統的控制問題。
評論