基于EKF的異步電機直接轉矩控制系統仿真研究
這樣就得到了離散化及線性化處理后的適合進行卡爾曼濾波運算的函數表達式,可以代入EKF算法進行迭代運算。
3 EKF建模與DTC系統仿真
本文的仿真和建模是在Matlab7.O的Simulink環境下完成的,主要包括異步電動機模型、轉矩調節器、磁鏈調節器、磁鏈自控制、開關信號選擇單元,其中擴展卡爾曼濾波模塊是由S函數編寫。
感應電機參數如下:定子自感Ls=0.610 8 H,轉子自感Lr=0.607 9 H,定、轉子互感Lm=0.593 2 H,定子相繞組電阻Rs=3.67 Ω,轉子相繞組電阻Rr=2.613 Ω,轉動慣量J=0.027 5kg·m2,極對數p=2。
為驗證該系統的精、動態性能,系統空載啟動,設定轉速為100 rad/s,進入穩定后,在t=0.5 s時加入負載TL=5 N·m,仿真圖如圖2~圖5所示。本文引用地址:http://www.104case.com/article/162474.htm
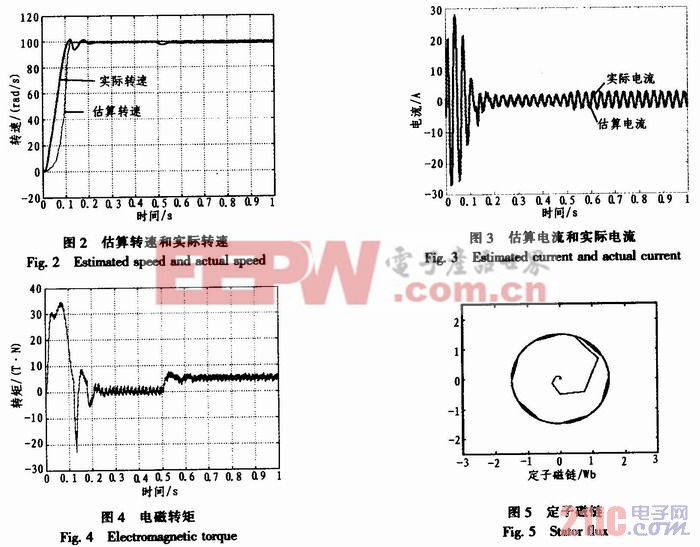
從仿真波形圖2對比可以看出,采用無速度傳感器控制算法后控制過程的上升時間比有速度傳感器控制稍微長一些,但仍能滿足系統性能指標要求。系統進入穩定后無速度傳感器控制的效果和有傳感器控制是一致的。圖4顯示的是突加負載后,從圖3看出定子電流幅值穩定,轉速變化很小并很快恢復穩定,輸出轉矩能很快達到給定負載轉矩,體現了DTC控制系統轉矩響應快的特點,由此可見電機在運行過程中,受到各種擾動時,電機轉速穩定性好,可以滿足對控制特性的要求。
EKF算法在異步電機轉子速度估計的應用過程中采用直接更新系統狀態量和協方差矩陣的方法,可以避免直接計算最大值動態范圍較大的增益矩陣Kk。利用EKF算法的關鍵在于協方差矩陣Q和R的選取。Q與模登誤差、系統分布、A/D量化誤差有關;R與電流傳感器噪聲以及A/D變換器的編碼誤差有關。
4 結論
從算法分析和系統仿真分析討論的結果,可以得出擴展卡爾曼算法在無速度傳感器應用中的優點是:利用擴展卡爾曼濾波器可以不必了解電機的機械參數知識(可以克服電機參數反應靈敏的問題),在電機啟動過程中不必知道電機轉子初始位置(可以解決電機的啟動問題),此外,EKF算法可以確保系統的全局穩定性(其他一些通過狀態觀測器實現電機無速度傳感器控制的方法,通常僅在標稱狀態的軌跡上將電機非線性化,不能保證系統的全局穩定性),而且整個系統易于數字化實現。但是擴展卡爾曼算法復雜,需要矩陣求逆運算,計算量大,為滿足實時控制的要求,需要高速,高精度的數字信號處理器。另一方面,擴展卡爾曼濾波器要用到很多隨機誤差的統計參數,由于模型復雜,涉及因素多,使得分析這些參數的工作比較困難,需要通過大量調試才能確定合適的隨機參數,而且調速范圍有一定的局限性,只適合中高速調速系統。
濾波器相關文章:濾波器原理
濾波器相關文章:濾波器原理
電源濾波器相關文章:電源濾波器原理
矢量控制相關文章:矢量控制原理 數字濾波器相關文章:數字濾波器原理




評論