基于神經網絡的微波均衡器建模與仿真

若考慮S2=1的情況，此時把整個神經網絡看成一個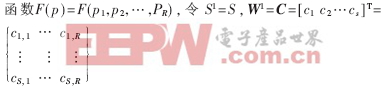

其中,ci(i=1,2,…,S)為矩陣C的每一行，它代表相應神經元徑向基函數的中心向量，b1=λ=(λ1,λ2，…λS),其中λi代表徑向基函數的方差，W2=W=(w1,w2,…,wS)，則網路輸出為：

2.2 網絡的訓練
　　僅僅搭建這樣一個模型是沒有意義的，神經網絡在實際工作之前必須進行學習，通過學習，神經網絡才能獲得一定的“智能”。
　　學習是神經網絡一種最重要也最令人矚目的特點。在神經網絡的發展進程中，學習算法的研究有著十分重要的地位。目前，人們所提出的神經網絡模型都是與學習算法相對應的。所以，有時人們并不苛求對模型和算法進行嚴格的定義或區分。有的模型可以有多種算法，而有的算法可能用于多種模型。
　　本文根據均衡器的傳輸特性，在訓練學習過程中，其連接權值的不斷調整以及學習修正采用BP網絡學習算法中的LM算法。LM算法是為了訓練中等規模的前饋神經網絡而提出的最快速算法，它對MATLAB實現也是相當有效的，在BP網絡的眾多學習算法中，通常對于包含數百個權值的函數逼近網絡，LM算法的收斂速度最快。如果要求的精度比較高，則該算法的優點尤其突出。在許多情況下，采用LM算法的訓練函數trainlm可以獲得比其他算法更小的均方誤差。
LM算法實際上是梯度下降法和牛頓法的結合。梯度下降法在開始的幾步下降較快，當接近最優值時，由于梯度趨于零，使得目標函數下降緩慢；而牛頓法可以在最優值附近產生一個理想的搜索方向。其主要算法為:

其中J是包含網絡誤差對權值及閾值的一階導數的雅可比矩陣。

牛頓法能夠更快更準確地逼近一個最小誤差，在每一步成功后，μ都會減小，只有當發現下一步輸出變壞時才增加μ。按這種方法，算法的每一步運行都會使目標函數向好的方向發展。
　　算法開始時，μ取小值μ=0.001。如果某一步不能減小E，則將μ乘以10后再重復這步，最后使E下降。如果某一步產生了更小的E，則將μ乘以0.1繼續運行。算法的執行步驟如圖3所示。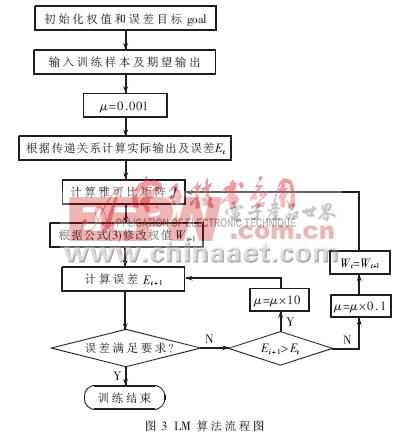

對于RBF網絡與BP網絡的主要區別在于使用不同的作用函數，BP網絡中的隱層節點使用的是Sigmoid函數，其函數值在輸入空間中無限大的范圍內為非零值。而RBF網絡的作用函數為高斯函數，因而其對任意的輸入均有高斯函數值大于零的特性，從而失去調整權值的優點。但加入LM算法進行網絡訓練后，RBF網絡也同樣具備局部逼近網絡學習收斂快的優點，可在一定程度上克服高斯函數不具備緊密性的缺點。由于RBF網絡采用高斯函數，表示形式簡單，即使對于多變量輸入也不增加太多的復雜性。
2.3 仿真設計結果