BTS 系統(tǒng)中開(kāi)環(huán)和閉環(huán) MIMO 的應(yīng)用
傳統(tǒng)方法中,接收機(jī)(Rx)和發(fā)射機(jī)(Tx)不會(huì)進(jìn)行往復(fù)通信。Rx需單獨(dú)計(jì)算出信道信息,解碼數(shù)據(jù)流。這給Rx造成了沉重而復(fù)雜的負(fù)擔(dān),也使系統(tǒng)無(wú)法完全利用信道的分集或容量。這些系統(tǒng)被稱(chēng)為開(kāi)環(huán)系統(tǒng)。
本文引用地址:http://www.104case.com/article/157672.htm最新的無(wú)線(xiàn)標(biāo)準(zhǔn)是在手機(jī)和基站(BTS)之間分配一個(gè)有限的反饋信道。這一信道有多種用途,特別是將信道的重要信息發(fā)送回BTS。該信息可實(shí)現(xiàn)簡(jiǎn)單的空間分集和復(fù)用技術(shù),后者增加了系統(tǒng)的有效信噪比(SNR),并潛在性地簡(jiǎn)化了Rx架構(gòu)。這些系統(tǒng)稱(chēng)作閉環(huán)系統(tǒng)。
學(xué)術(shù)文獻(xiàn)對(duì)理論限制進(jìn)行了大量研究,卻很少涉及電路實(shí)現(xiàn)復(fù)雜性方面的內(nèi)容。本文將講述MIMO開(kāi)環(huán)和閉環(huán)技術(shù)如何在復(fù)雜度和性能之間進(jìn)行權(quán)衡,并提供實(shí)際系統(tǒng)的經(jīng)驗(yàn)法則。
開(kāi)環(huán)MIMO
對(duì)于單發(fā)射天線(xiàn)或SIMO系統(tǒng),Rx利用MRC技術(shù)整合來(lái)自多個(gè)接收天線(xiàn)的數(shù)據(jù)流,以實(shí)現(xiàn)分集增益。而多個(gè)發(fā)射天線(xiàn)的信道更復(fù)雜,兩個(gè)不同的傳輸流間會(huì)出現(xiàn)干擾。如果Tx沒(méi)有信道信息,Rx單獨(dú)使用MIMO容量,這通常需要非常復(fù)雜的算法。
空間復(fù)用
空間復(fù)用是一種非常著名的開(kāi)環(huán)MIMO技術(shù),廣泛應(yīng)用于無(wú)線(xiàn)系統(tǒng)。每個(gè)發(fā)射天線(xiàn)送出不同的數(shù)據(jù)流。
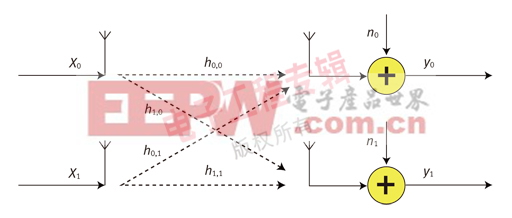
圖1:2x2 空間復(fù)用系統(tǒng)。
圖1是一個(gè)2x2的空間復(fù)用系統(tǒng),可以建模為:
(1)
其中x代表發(fā)射信號(hào)向量,H代表信道矩陣,n代表增加的噪聲向量,y代表接收信號(hào)向量。為了根據(jù)接收信號(hào)y評(píng)估發(fā)射信號(hào)x,直接的方法就是用迫零(zero forcing)或MMSE等逆信道矩陣乘以y。然而,這并非最佳檢測(cè)方法。
最理想的檢測(cè)方法可利用最大似然法(ML)準(zhǔn)則。在大多數(shù)情況下,發(fā)射信號(hào)向量最大限度縮短了與接收信號(hào)向量y相關(guān)的歐幾里得距離,因此,可以通過(guò)尋找發(fā)射信號(hào)向量來(lái)執(zhí)行最大似然法。
(2)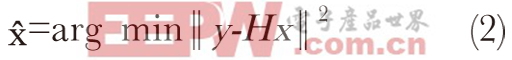
可惜,計(jì)算的復(fù)雜性也隨著發(fā)射天線(xiàn)和可能的星座點(diǎn)的數(shù)量呈指數(shù)增加,這使最大似然法無(wú)法適于實(shí)際用途。
球形解碼(sphere decoding)雖然不是最理想的ML解決方案,卻是一種廣泛使用的方法。球形解碼算法的原理,是在球半徑內(nèi)搜索離接收信號(hào)最近的格點(diǎn)。在球半徑內(nèi),格點(diǎn)場(chǎng)的每個(gè)格點(diǎn)都代表一個(gè)碼字。球形解碼顯著降低了檢測(cè)的復(fù)雜性,其性能可與ML檢測(cè)方法相匹敵。
然而,盡管球形解碼算法已經(jīng)降低了復(fù)雜性,卻不適于實(shí)施大量天線(xiàn)和64QAM等高調(diào)制率。
空時(shí)碼
另一個(gè)廣泛采用的開(kāi)環(huán)MIMO是空時(shí)碼。利用空時(shí)碼,一個(gè)數(shù)據(jù)流可以用多個(gè)發(fā)射天線(xiàn)傳輸,但是信號(hào)編碼利用多個(gè)天線(xiàn)中的獨(dú)立衰落,以實(shí)現(xiàn)空間分集。
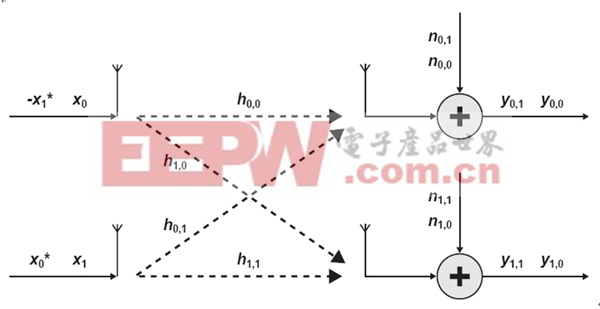
圖2:典型的Alamouti碼。






評(píng)論