RS通信編碼器的優化設計及FPGA實現

引言
Reed-Solomon碼首先是由Reed和Solomon兩人于1960年提出來的，簡稱為RS碼。這是一類具有很強糾錯能力的多進制BCH碼，既能糾正隨機錯誤，也能糾正突發錯誤，也是一類典型的代數幾何碼。RS碼一直以來都是國際通信領域研究的熱點之一。
本文以戰術軍用通信系統的首選碼RS(31，15)碼為例，對生成多項式進行了優化，并采用查表法的原理極大地提高了編碼器運算數據的能力，縮短了運算周期，最終利用VHDL語言編譯，在FPGA中實現，得到了正確的RS編譯碼。

1 RS編碼原理
能糾正t個錯誤的RS(n，k)碼具有如下特性：
碼長：n=2m-1符號或m(2m-1)比特；信息碼元數：k=n-2t符號或mk比特；監督碼元數：n-k=2t符號或m(n-k)比特；最小距離：d=2t+1=n-k-1符號或m(n-k+1)比特；最小距離為d的本原RS碼的生成多項式一般為：

令信息元多項式為：

監督多項式為：

則碼多項式為：

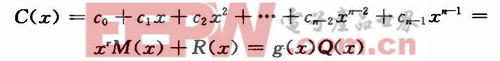
式中：Q(x)是g(x)整除C(x)所得的商式。所有這些原理都與二進制循環碼一樣，不同的僅在于運算方法。對于二進制碼，碼多項式各項系數只能取0或1，多項式的加減乘除是模二運算，是定義在GF(2)域上的多項式。現在碼多項式各項系數可以取q=2m種不同的值，應當是定義在GF(2m)域上的多項式。

2 生成多項式的優化
以RS(31，15)為例，n=31，k=15，可糾正錯誤數為t=(n-k)／2=8；以為本原多項式，可得到GF(25)上的元素如表1所示。
一般的生成多項式為：

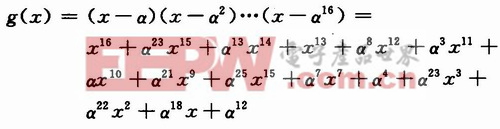
則碼字多項式以為零點。
由于注意到：