基于改進平衡Winnow算法的短信過濾系統
加入技術交流群
2 構造分類器
訓練分類器是研究的重點，采用Balanced Winnow 算法并對其進行改進。
2.1 Winnow 分類算法
Winnow 算法是二值屬性數據集上的線性分類算法。線性分類問題中表示分類界限的超平面等式如下：
w0α0+w1α1+w2α2+…+wkαk=0 ， 其中：α0，α1，…，αk分別是屬性的值；w0，w1， …，wk是超平面的權值。如果其值大于0 ， 則預測為第一類否則為第二類。
Winnow 算法是錯誤驅動型的分類算法， 即當出現錯分的實例時才更新權值向量。設定兩個學習系數α 和β(其中α＞1，β＜1) ， 通過將權值乘以參數α( 或β) 來分別修改權值。
2.2 Balanced Winnow 分類算法
標準的Winnow 算法不允許有負的權值， 于是就有了另一個稱為平衡的Winnow 版本， 允許使用負的權值。
對Winnow 算法的基本形式， 權重向量的每一維都是正數。Balanced Winnow 是用w+-w-代替w， 當
則將實例歸為該類。Balanced Winnow 的權重更新策略為：(1) 如果
， 但文本不屬于該類， 則要降低權重： 對j=1，，…，d，如果xj≠0 ， 則xj≠0 ， w+j =βw+j ，w-j =αw-j ，α＞1，0＜β＜1。(2) 如果
但文本應屬于該類， 則要提高權重： 對j=1，2，…，d，如果xj≠0， 則w+j =αw+j ，w-j =βw-j ，α＞1，0＜β＜1。在實驗中， 采用文獻[7] 中統一α 和β 為一個參數的方法， 令β=1/α， 沒有影響分類效果， 但有效簡化了參數的選擇?？梢詾椴煌念悇e確定不同的θ 值， 但實驗表明： 對于不同的類別選擇同樣的θ 值， 結果幾乎是一樣的， 所以在每次獨立的實驗中都取相同的θ 值， 大小是訓練文本所含的平均特征數， 而初始的w+和w-分別取全2 和全1 向量。
在平衡Winnow 算法中， 一旦參數α、β 和閾值θ 確定下來后， 將在訓練過程中不斷更新權重向量w+和w-至最適合這組參數。因此對參數的依賴較小， 需要手工調整的參數不多。
2.3 去除野點
在短信過濾中，短信樣本是由手動或自動方式收集的， 收集的過程中難免會出錯， 因此短信樣本集中可能存在一些被人為錯分的樣本點， 即野點。這些野點在訓練時， 會使得分類器產生嚴重的抖動現象， 降低分類器的性能。因此，好的分類器應具有識別野點的能力。
對于Winnow 算法，若樣本中存在野點， 則野點在訓練時以較大的概率出現在兩分類線之外， 且分類錯誤。
這些野點對分類器的訓練過程產生很大的影響， 可能會造成分類器的“ 過度學習” 。因此引入損失函數， 按照損失函數的定義， 這些野點損失較大， 因此可以通過給損失函數設置一個上界函數來處理線性分類器中的野點問題， 如圖1 所示。
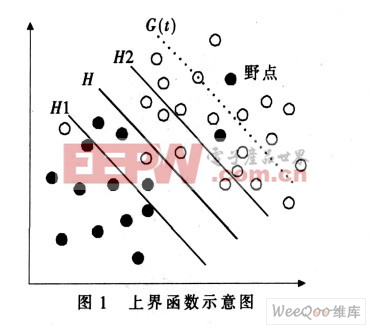
圖1 所示為兩類線性可分情況， 圖中實心點和空心點分別表示兩類訓練樣本，H 為兩類樣本沒有被錯誤地分開的分類線，H1 和H2 分別為平行于分類線H 且與分類線H 的距離為單位距離的兩條直線。直線G(t)為平衡Winnow 算法中第t 輪迭代后損失函數的上界線。該上界線是關于迭代次數t 的函數， 因此可以將該上界線G(t)對應的上界函數記為g(t)。從圖1 可知， 在直線G(t)左下側誤分樣本的損失較少， 可以認為這些誤分樣本是由于當前分類器的性能較低而誤分的； 在直線G(t) 右上側誤分的樣本由于在第t 輪迭代后損失仍較大， 則可以認為這些誤分的樣本是野點。根據線性分類器和野點的性質可知，上界函數g(t)具有以下性質：
(1) 隨著Winnow 算法中迭代次數t 的增加， 上界函數g(t) 單調遞減， 并且遞減的速率也隨著t 的增加而遞減， 即上界函數的導數g(t)為單調遞減函數；(2) 上界函數既不能太大， 也不能太小。太大會降低判斷野點的能力， 太小則會誤判正常樣本為野點。
根據上界函數的這些特性， 可以考慮一個平行于分類線H 的線性函數作為損失函數的上界函數。即g(t)=
其中：ε 為常數值； 直線G(t) 平行于分類線H；η 為損失因子， 也稱為學習率， 可以在訓練分類器的時候指定其值。在每一輪訓練中， 若該樣本的G(t) 值大于分類線的值， 并且超過一定的閾值， 且不屬于該類， 則判定該樣本具有野點的性質， 應當在訓練集中將該樣本去除， 以便提高下一輪訓練的準確性。這樣不僅有效削弱了分類器的抖動現象， 而且提高了分類器的性能。
評論