擴頻信號基于FFT碼捕獲的計算量分析
1.2.1 基本原理
循環相關捕獲的示意圖如圖2所示,它是在時域中表示的,且只給出21個本地碼的其中一個。如果用5 MHz對輸入信號采樣,輸入電文長1 ms,含有5 000個數據點。可以認為輸入電文與本地電文位于兩個圓柱體表面,為了去匹配輸入電文,本地碼要旋轉5 000次。換句話說,一個圓柱體相對于另一個圓柱體旋轉5 000次。本文引用地址:http://www.104case.com/article/153638.htm
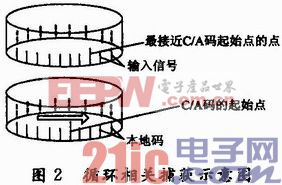
在每一步,5 000個輸入電文與5 000個本地電文點對點相乘,相乘結果加到一起。包含本地碼與輸入碼所有可能的乘積需要5 000步,乘積中最高幅值被記錄下,若大于門限值,就是我們的期望值。
從基本原理上講,這種方法與滑動相關法是等同的,都是通過滑動碼片來尋找最大值。不同的是,循環相關法每一次滑動后不用逐一相乘后相加,而是將時域信號進行快速傅里葉變換(FFT)轉換成頻域信號,在頻域中求循環相關運算,直接求出了5 000次滑動中每一次滑動的相關值。在硬件實現中,可以利用自帶的IP核直接進行FFT運算,這大大節約了資源。FFT的運算量分析在后文中將進行介紹。
1.2.2 具體步驟
采用如上所述的基于FFT的循環相關捕獲方法,假定捕獲的頻率搜索范圍是±10 kHz,步進1 kHz,總共有21個頻率分量。本地碼lsi可表示為:
![]()
式中:下標s代表衛星編號,下標i=1,2,…,21,Cs是衛星s的C/A碼,fi=fc,-10,-9,…,9,10 kHz。這21組數據代表了間隔1 kHz的21個頻率。將他們與輸入信號進行相關運算,如果本地產生信號的C/A碼和頻率都正確的話,當C/A碼相位對準時,輸出達到峰值。
對輸入數據進行捕獲操作的具體步驟如下:
(1)對1 ms的輸人數據x(n)進行FFT變換,將輸入數據變換到頻域X(k),n=k=0~4 999;
(2)取X(k)的復共軛,值為X*(k);
(3)用式(2)生成21個本地碼lsi(n),i=1,2,…,21。每個lsi(n)都有5 000個數據點。
(4)對lsi(n)取FFT,轉換為頻域中的Lsi(k)。
(5)將Lsi(k)與X*(k)逐點相乘,結果為Rsi(k)。
(6)求Rsi(k)的FFT逆變換,變換到時域rsi(n),求絕對值|rsi(n)|,總共有105 000(5 000×21)個|rsi(n)|。
(7)在輸入電文200 ns的時間分辨率和載波頻率為1 kHz分辨率的條件下,|rsi(n)|最大值中的第n位和第i個載波頻率給出了C/A碼的初始點。
圖3給出了基于FFT的捕獲流程示意圖。
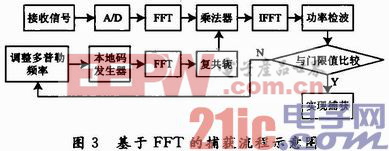
2 不同捕獲方法的計算量比較
從理論上講,滑動相關法與基于FFT的循環相關捕獲法都是利用數據點進行相關計算并比較求得最大值。其不同之處在于計算量的差距上,采用基于FFT的循環相關法計算量大大的減少,下面對其進行分析。
2.1 傳統滑動相關法
使用傳統滑動相關法進行捕獲,考慮21個多普勒頻率分量,由于它們進行相同的操作,只對這21組數據的某一組進行討論。
輸入數據和C/A碼各含有5 000個數據點,根據滑動相關法的原理,要將C/A碼滑動5 000次,每滑動一次碼片都要將C/A碼與數據進行5 000點的復乘,這樣,在每個頻率分量上要進行5 000×5 000次乘法運算,則21個頻率分量共進行:
S=5 000×5 000×21=5.25×108 (3)
次運算。由此可見,這種方法在硬件實現中非常浪費資源。
2.2 基于FFT的循環相關法
2.2.1 FFT算法計算量簡介
采用快速FFT/IFFT運算,可以顯著降低運算的復雜度,在這里簡單介紹一下如何計算IFFT的運算量。FFT的運算量與此相同,不做贅述。
對于常用的基2IFFT算法來說,其復數乘法的次數僅為(N/2)log N。隨著N的增加,算法復雜度之間的差距越明顯,IDFT的計算復雜度會隨著N的增加而呈現二次方增長,IFFT的計算復雜度的增加速度只是稍微快于線形變化。
對于計算點數比較多的系統,可以采用基4FFT算法。在4點的IFFT運算中,只存在與{1,-1,j,-j)的相乘運算,因此不需要采用完整的乘法器來實施這種乘法,只需要通過簡單地加、減以及交換實部和虛部的運算(當與-j,j相乘時)來實現這種乘法。在基4算法中,IFFT變換可以被分為多個4點的IFFT變換,這樣就只需要在兩個級別之間執行完整的乘法操作。因此,N點的基4IFFT算法中只需要執行(3/8)·N·(log N-2)次復數乘法或相位旋轉,以及N·log N次復數加法。








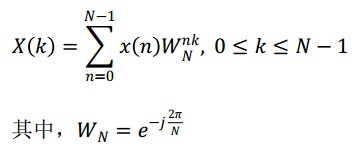
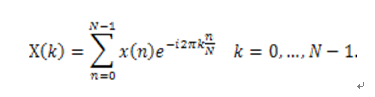
評論