基于嵌入式測控系統的數字濾波方法設計

　　算術平均濾波和去極值平均濾波均存在平滑性和靈敏性的矛盾。因為，采樣次數太少，平滑效果差；采樣次數太多，靈敏度下降，對參數的變化趨勢不敏感。為協調兩者的關系，可采用加權平均濾波。即對連續N次采樣值分別乘上不同的加權系數之后再求累加和。加權系數一般先小后大，以突出后面若干采樣的效果，來加強系統對參數變化趨勢的辨識。各個加權系數均應是小于1的小數，且應滿足總和等于1的約束條件。這樣，加權運算之后的累加和即為有效采樣值。為方便計算，可取各加權系數均為整數，且總和為256，加權運算之后的累加和再除以256后便是有效采樣值。其參考程序如下：

　1.6滑動平均濾波

　　以上介紹的各種平均濾波算法具有一個共同點，即每取得一個有效采樣值都必須連續進行若干次采樣，這些方法在采樣速度較慢(如雙積分型A／D轉換)或目標參數變化較快時，系統的實時性往往不能得到保證。而滑動平均濾波算法只采樣一次，它將這一次采樣值和過去的若干次采樣值一起求平均，然后所得到的有效采樣值即可投入使用。這樣，如果取N個采樣值求平均，則RAM中必須開辟N個數據的暫存區。每新采集一個數據便存入暫存區，同時去掉一個最老的數據，以保持這N個數據始終是最近的數據。這種數據存放方式可以用環形隊列數據結構來實現。其參考程序如下：

　　1.7低通濾波

　　將普通硬件RC低通濾波器的微分方程用差分方程來表示，便可用軟件算法來模擬硬件濾波功能。經推導，對于低通濾波算法有：

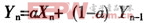
　　式中Xn為本次采樣值；Yn-1為上次的濾波輸出值；α為濾波系數，其值1；Yn為本次濾波輸出值。這種算法對變化緩慢的物理量是很有效的。但應注意一點，它不能濾除高于二分之一采樣頻率的干擾信號。比如采樣頻率為2 Hz，則對1 Hz以上的干擾信號通常應配合硬件濾波電路來濾除。該方法的參考程序如下：

　　2各種數字濾波方法對比

　　數字濾波的方法多種多樣，表1給出了幾種數字濾波算法的優缺點和適用對象。

　　3 結束語

　　基于嵌入式測控系統的數字濾波方法多種多樣，因此，在選擇濾波方法時，首先要考慮微控制器的存儲量、運算時間、運算能力以及實時性是否滿足實際要求。然后再根據主要的干擾源(對系統的測試精度影響最大的干擾源)和測試對象的特點來選擇合適的濾波方法。