如何制作動畫程序
使用Canvas類的isDoubleBufferd()方法就能知道是否適應雙緩沖存儲器。由于使用這種方法可以區分開適應雙緩沖存儲器的情況和不適應適應的情況,因此無論在什么樣的環境下都能夠有效控制閃爍現象。示例如下:(ex.6)
classDoubleBufferdCanvasextendsCanvas{
ImageoffImg=null;//關閉畫面的圖片
/**
*表示canvas之前所運行的方法
*/
protectedvoidshowNotify(){
if(!isDoubleBuffered()){//關閉畫面的圖片
offImg=Image.createImage(getWidth(),getHeight());
}
}
/**
*描繪方法
*/
protectedvoidpaint(Graphicsg){
Graphicsbg=null;
if(offImg!=null){
bg=offImg.getGraphics();
}else{
bg=g;
}
//使用bg描繪
bg.setColor(255,255,255);
bg.fillRect(0,0,getWidth(),getHeight());
bg.setColor(255,0,0);
bg.drawArc(x,y,30,30,0,360);//描畫圓
//將offscreenimage導入畫面
if(!isDoubleBuffered()){
g.drawImage(offImg,0,0,Graphics.TOP|Graphics.LEFT);
bg=null;
}
}
}
ex.6
4-3-1時鐘的應用程序
那么,現在我們就作為示范使用動畫制作應用程序吧。在本講中將要制作的應用程序就是模擬表應用程序。利用秒表,描繪出模擬表。在描繪模擬表針時使用三角函數。類結構表如下:(表2)

Table2
4-3-2時間的設定
在模擬表應用程序中秒針一秒動一下。因此,使用秒表,要設定每秒不同時刻的畫面更新。在ClockCanvas類的paint方法內取得時刻,描繪鐘表。秒表任務如下所示:(ex.7)
/**********************************************
*秒表任務
**********************************************/
classClockTimerTaskextendsTimerTask{
privateClockCanvascanvas;
/**
*構造函數
*/
publicClockTimerTask(ClockCanvascanvas){
this.canvas=canvas;
}
/**
*在每個指定時間內運行
*/
publicvoidrun(){
canvas.repaint();//再次描繪canvas
}
}
ex.7
定義完秒表任務后,就要在秒表上設定秒表任務。用ClockCanvas類的構造函數進行如下設定。(ex.8)
/**
*構造函數
*/
publicClockCanvas(){
//設定秒表
timer=newTimer();
timerTask=newClockTimerTask(this);
timer.schedule(timerTask,1000,1000);//Onceevery1,000ms
}
ex.8
4-3-3描畫鐘表
設定完秒表后開始描繪鐘表。下面就是鐘表的框架(clock.png)。(圖4)

Figure4
接下來描畫秒針。因為要根據時刻變化秒針的位置,所以有必要根據時刻計算秒針的位置。在這兒用Graphics類的drawLine方法描繪秒針。在表的中心坐標上固定住線的始點,從時刻中計算出線的終點。
使用三角函數計算秒針終點的坐標。表的中心坐標是(x,y)、秒針的長度設為1,秒針的角度設為θ,那么終點的坐標就是(x+l*cos(θ),y+l*sin(θ))。(圖5)
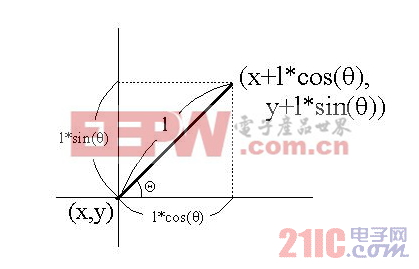
Figure5
三角函數的實際計算,在J2SE中,Math類有sin,cos方法,所以通常會使用這些方法,而J2ME中是沒有這種方法的。因此,在本講中定義了名為TrigonometricFunctions的類,將預先計算好的sin,cos值擴大10000倍排列并保持在這個類中。所謂擴大10000倍,是由于J2ME不支持double和float等小數點型,所以不能原封不動地保存小數點sin,cos。因此,用MIDP處理小數時,將小數擴大幾倍變成整數加以保持,實際上在使用時,用事先乘出的數值再除以所乘的數值,計算并使用由此而得出的實際值。
然而,在J2ME下處理含有小數的數值時,由于要將小數四舍五入成整數所以就會產生誤差。例如:0.12341234…四舍五入成整數就是0,這與原來的0.12341234…是有誤差的。由于要盡量減少誤差,所以計算之前要盡可能的乘以大數值并且有必要保存其整數。例如:在先前的0.12341234…基礎上乘以1000后就變成了123.41234…,小數點以下四舍五入后就是123。將123除以1000后就是0.123。這與開始的數值之間的誤差僅為0.00041234…,原封不動的將原來的數值四舍五入后數值0產生的誤差是0.00041234…,二者相比則前者的誤差要小的多。總之,小數上乘以的數值越大四舍五入后與原來的數值之間的誤差就越小。
先講sin,cos的數值擴大10000倍,秒針坐標計算的最后在除以10000。N800畫面尺寸的縱長為180,那么進行180*x(只有X為小數)計算時的最大誤差是
0.0000999...*180=0.017999...isapproximately0.0180
總是比1小,沒有四舍五入的誤差。
接下來描繪秒針。SecondAngle作為秒針的角度,SECOND_LENGTH是秒針的長度,表的中心坐標是(CENTER_X,CENTER_Y)。(ex.9)
intsecondX=CENTER_X+TrigonometricFunctions.COS[secondAngle]*SECOND_LENGTH/10000;
intsecondY=CENTER_Y-TrigonometricFunctions.SIN[secondAngle]*SECOND_LENGTH/10000;
g.drawLine(CENTER_X,CENTER_Y,secondX,secondY);
ex.9
下面是ClockCanvas類的源碼。畫面上有表的中心坐標。
importjava.util.*;
importjavax.microedition.lcdui.*;





評論