藥品質量穩定性的量化分析

　　藥品生產是一個系統工程，在這樣一個復雜的系統工程中，存在許多不確定因素，哪怕是最先進的制藥公司都可能會對其中的一些因素沒有完全掌握。隨著藥品GMP法規的實施，以及國內外各種認證的要求，對歷史數據的統計分析逐步被制藥企業和官方藥品檢定機構所重視，并日漸成為監控藥品質量的必備分析技術。

　　但是一說起統計分析，不少人就會退避三舍，敬而遠之。其實，隨著計算機信息技術的飛速發展，非統計專業背景的分析人士進行專業統計分析已經不是什么稀罕的事情。下面就用一個發生在藥品質量穩定性分析領域的實際案例來說明如何借助權威統計分析軟件JMP在醫藥公司中推廣和應用統計分析技術。

　　某藥廠想根據試生產的三批鹽酸特拉唑嗪膠囊來了解新藥品的有效期。取樣的樣品為氣泡眼鋁塑包裝，放置于濕度為RH70%、溫度為25℃的條件下。分別在0月、1月、2月、3月、6月、9月后觀察樣品的外觀、有關物質、溶出度及含量變化。試根據檢定結果，預測該藥品在25度下的有效期(指含量降解至90%所需的時間)。

　　如下圖所示，共顯示了3個列變量、18條行記錄保存在JMP軟件的數據表中，其中第一列表示不同的藥品批號;第二列表示這批藥品的貯存時間(月);第三列表示這批藥品貯存若干個月后的含量值。

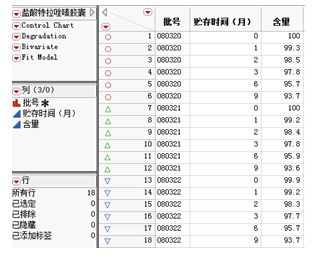
　　圖一 鹽酸特拉唑嗪膠囊的檢測數據

　　首先，想大致了解一下藥品含量的穩定性如何。根據數據的特征，選擇單值控制圖來進行圖形化分析。從用JMP軟件繪制出來的下圖可知，所有批次的藥品含量都很不穩定，而且隨著貯存時間的延長明顯地下降，尤其是貯存9個月后，含量都已經低于控制下限了。

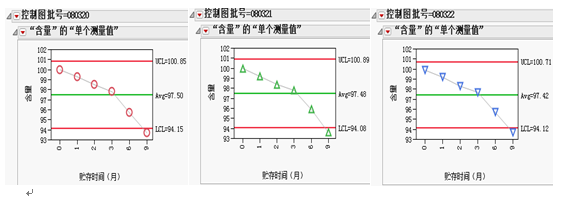
　　圖二 不同批號“含量”的單值控制圖

　　接著，想更加量化地研究藥品含量與存貯時間的關系。這時，回歸分析中的簡單線性回歸是個很合適的分析工具。我們可以為三個批號的藥品分別構建一個回歸模型，也可以將這三個批號的藥品看作一個整體，只構建一個單一的回歸模型。經過用JMP軟件分析得到不同模型的比較檢驗(如下圖所示)，發現可以用相同的截距和斜率來表達三個批號的藥品。因此，決定選擇第二種回歸分析方式。

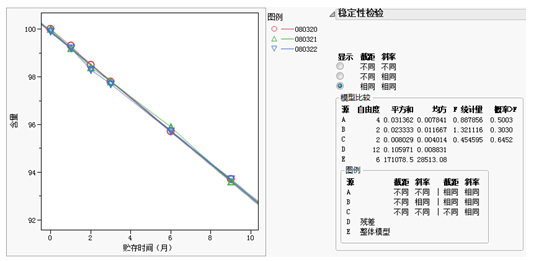
　　圖三 不同批號“含量”的簡線性回歸模型比較

　　然后，針對所有數據，用JMP軟件構建出一個簡單線性回歸模型(如下圖所示)，即含量 = 99.893333 - 0.6933333*貯存時間(月)。從擬合匯總、方差分析的報表來看，該模型是成立的，具有顯著的統計學意義。這個模型的實際意義是：總體而言，每過1個月，藥品含量平均會下降0.69個百分比。

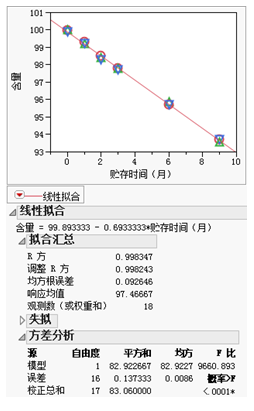
　　圖四 “含量”的總體簡單線性回歸模型

　　最后，再用JMP軟件基于前面得到的回歸模型進行反向預測(如下圖所示)，可以求得含量降解到90%時，需要經過的平均時間是14.26個月，這個時間95%的置信區間是14.03到14.52個月。因此，我們可以更保守、同時也更有把握地說：該藥品在40度下的有效期是14個月。

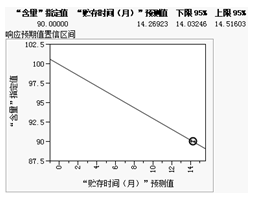
　　圖五 “含量”回歸模型的反向預測

　　坦率地說，目前我國醫藥企業的質量管理層次還不夠高，很多統計質量管理工具的應用水平與國外同類企業相比還有很大的差異。希望此文能對趨勢分析技術在今后藥品領域中的應用和推廣起到拋磚引玉的作用，進而讓更多的人重視和熟練使用該技術，使其更好地服務于藥品質量的監控與提高。