獨家｜OpenCV 1.7 離散傅里葉變換

目標

本小節將尋求以下問題的答案：

什么是傅立葉變換，為什么要使用傅立葉變換？

如何在OpenCV中使用傅立葉變換？

 copyMakeBorder() , merge() , dft() , getOptimalDFTSize() , log() 和 normalize() 等函數的使用方法。

源代碼

可以到

samples/cpp/tutorial_code/core/discrete_fourier_transform/discrete_fourier_transform.cpp目錄下查看OpenCV的源代碼庫。

下面是dft（）的應用示例程序：

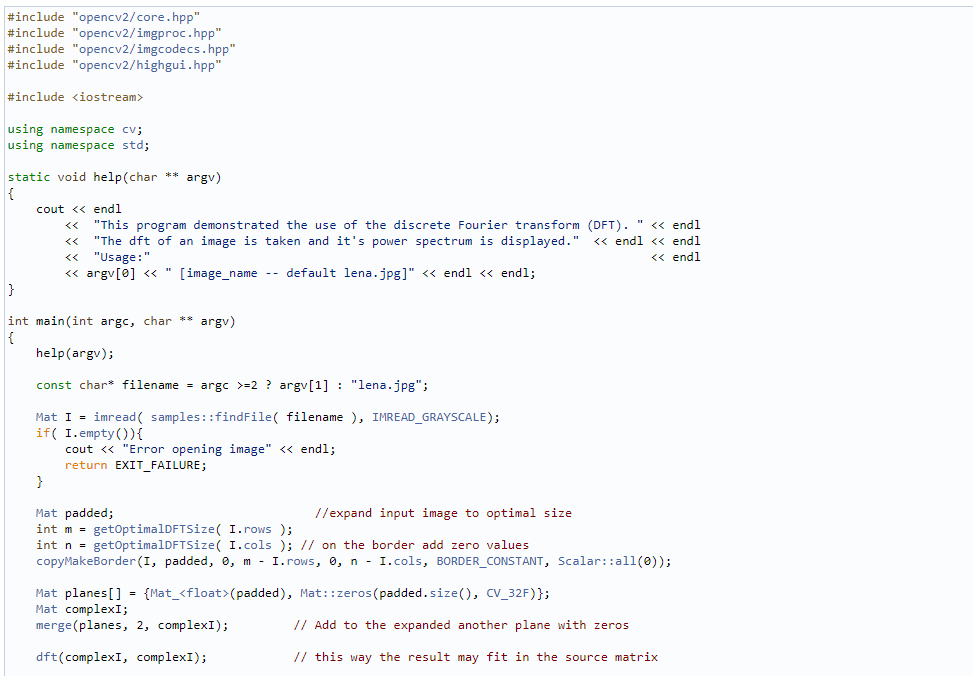
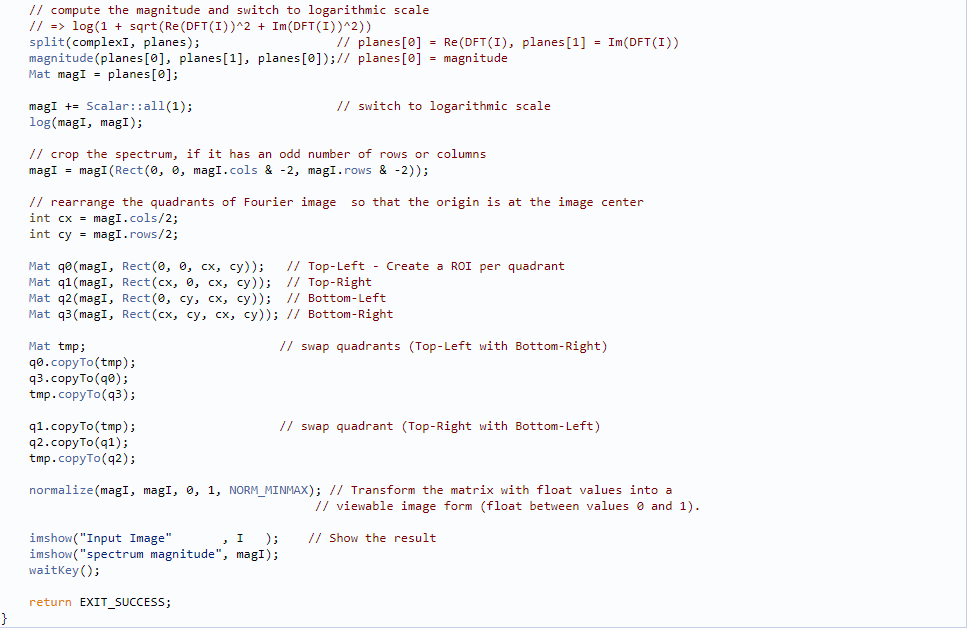
代碼詳解

傅立葉變換可以將圖像分解成正弦和余弦分量。也就是說，它將圖像從空間域變換到頻率域。其主要思想為：任何函數均可以用無限多個正弦和余弦函數之和來精確近似。傅立葉變換正是這一想法的實現。數學上，一張二維圖像的傅里葉變換可表示如下：

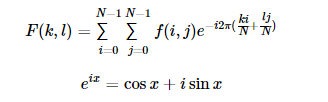
這里，f是圖像在空間域的圖像值， F是圖像在頻率域的圖像值，轉換后的結果為復數，可以通過并且可以用實數圖和復數圖進行表示，也可以用幅度和相位圖進行表示。然而，對于圖像處理算法而言算法僅關注圖像的幅度信息，因為其中包含了圖像幾何結構中的所有信息。如果想通過對復數圖像或幅度/相位圖像下的象函數進行修改，從而間接地調整原函數， 那么則需要保留象函數的值，并進行傅里葉變換逆變換，從而獲得調整后的原函數的數值。

在此示例中，將介紹如何計算和顯示圖像經過傅里葉變換的幅度圖值。假設數字圖像的傅里葉變換是離散的傅里葉變換，可以在給定的域值中任取一個數值。例如，灰度圖像的像素值通常在0到255之間，那么傅立葉變換的結果也是離散型的。當需要從幾何視角來確定圖像的結構時，便可適用DFT。下面是離散型的傅里葉變換（DFT ）的實現步驟（假設輸入圖像為灰度圖像I）：

將圖像展開到最佳尺寸

DFT的性能取決于圖像的大小，當圖像的尺寸為2，3，5 的倍數時，離散傅里葉變換（DFT ）的速度最快。因此，為獲得最優的性能，可以通過調整圖像的邊界值來獲得便于快速計算的圖像尺寸。getOptimalDFTSize（）函數返回一個最優尺寸的圖像，使用copyMakeBorder（）函數擴展圖像（將增加的像素值初始化為零）的邊界：

為復數的實部和虛部開辟存儲空間

傅立葉變換的結果是復數，這意味著，每個圖像對應著兩個像素值（實部和虛部各一個分量）。此外，頻率域范圍比其對應的空間域范圍要大得多，所以至少要用浮點（float format）的格式來存儲傅里葉變換的結果。為此，需要將輸入的圖像數據類型轉換成浮點類型，并擴展出另一個通道來保存復數值：

離散傅立葉變換

進行原位計算（輸入數據同輸出數據）：

將復數的實部和虛部轉換成幅度值

復數包含實部(Re)和虛部( Im) 兩部分。DFT的結果為復數，這個復數的幅度為：

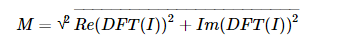
轉換成OpenCV的代碼如下：

切換到對數尺寸

由于傅里葉系數的動態范圍過大，無法在屏幕上顯示，

一些較小和較大的變化值也無法在線性尺度下觀察到。因此，較高的數值會變成白點，而較小的數值變為黑點。為了便于顯示全部數值，可使用灰度值，并將線性尺寸變換成對數尺寸：

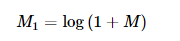
轉換成OpenCV代碼如下：

剪裁和重排

在上述第一步中，對圖像的尺寸進行了擴展，在這里則需要拋棄由圖像擴展而新引進的像素值。為了方便可視化，對結果值的象限重新排列，使得原點（零，零）對應圖像中心。

歸一化

歸一化的目的也是為了便于可視化。經過運算之后，獲得了幅度值，但這些數值仍然超出了圖像的顯示范圍（從零到一），為此，利用cv::normalize()函數對幅度值進行歸一化，取值在零到一的范圍之內。

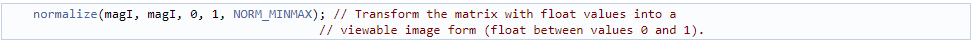
結果

應用傅里葉變換的主要目的是要確定圖像的幾何方向。例如，如何看出文本是水平還是垂直方向的？對于某些文字來說，文本行的排序形式是水平線，而字母則形成某種垂直線。經傅里葉變換后，仍然可以看到文本中片段中的兩個主要部分。下面，分別用水平和旋轉圖像來描述某一文本。

水平文本圖像：

旋轉文本圖像：

從中可以看出，頻域中影響最大的分量（幅度圖像上最亮的點）會隨著圖像的幾何位置旋轉，可以根據這一點計算出偏移量，通過旋轉圖像來對位置進行糾正。

注：本文以C++語言代碼為例，獲取Java和python版本可在原文中查看：

https://docs.opencv.org/4.5.2/d8/d01/tutorial_discrete_fourier_transform.html