【專】微觀電流——擴散電流
一、電流與速度
了解完電場作用下的漂移電流,接下來我們講解熱運動導致的擴散電流。
熱運動的最小自由空間為一個平均自由程,即一個粒子通過熱運動與相鄰粒子相碰撞的平均距離。假設在溫度T下,半導體中電子的平均自由程為l,熱運動平均速度為vth,熱運動通過一個平均自由程所需時間為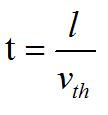 。
。
在一維情況下,假設沿x方向的電子濃度分布為n(x)。如圖所示“0”點所示位置,其距離最近的鄰近電子分別位于l和-l處,相應的電子濃度分別表示為n(l)和n(-l)。根據平均自由程的定義不難理解,最先可能擴散到“0”位置的電子就處于這兩個位置。
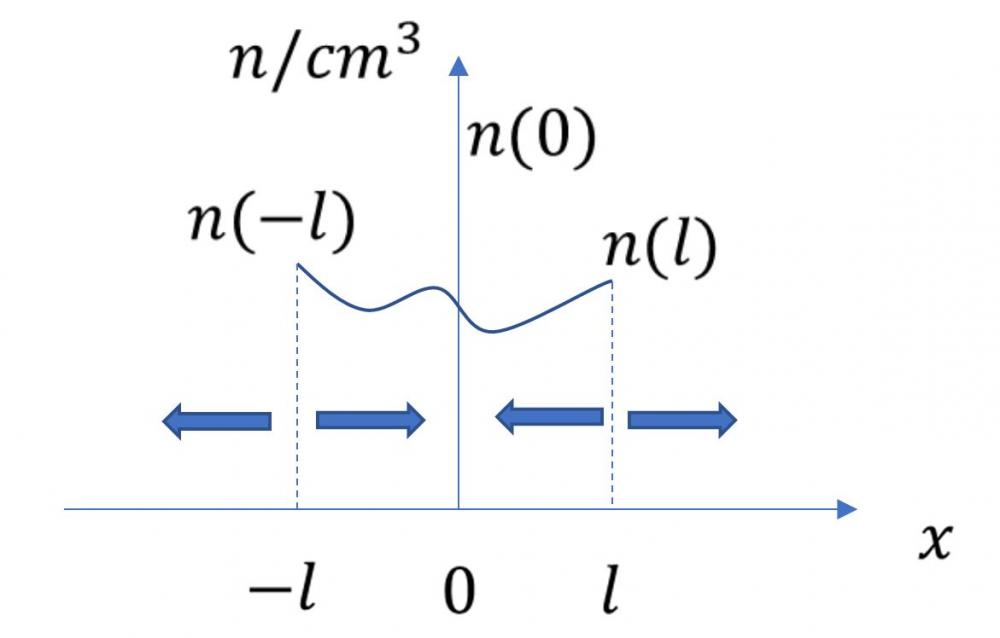
根據電流密度定義,要獲知“0”點的電流,就要計算左右兩側n(l)和n(-l)分別在t時間內通過“0”點的電荷總量。
以-l位置的n(-l)個電子為例,在一維狀況下,這些電子熱運動往左或者往右的概率相同,均為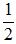 。所以,在單位時間內通過“0”點的電荷數量為
。所以,在單位時間內通過“0”點的電荷數量為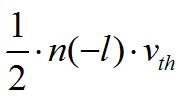 ,相應產生電流為:
,相應產生電流為:
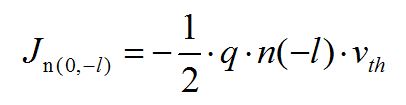
(設電流以x方向為正,添加“-”的原因是電子電流方向與運動方向相反)同理,對于l位置的n(l)個電子在“0”點產生的電流為:
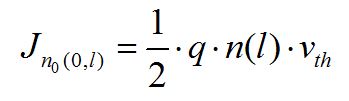
n(l) 和n(-l)在“0”點產生的總電流為:
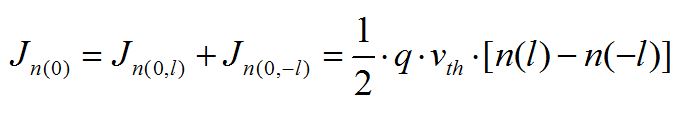
這樣,我們就能得到電流J與速度v之間的關系。
二、電流、速度和濃度梯度
進一步地,我們想要梳理清楚電流、速度和濃度梯度之間的關系。
一維濃度梯度的表達方式為濃度n(x)在x方向上的微分,即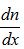 。根據Jn(0)的表達式,只需梳理[n(l)-n(-l)]與
。根據Jn(0)的表達式,只需梳理[n(l)-n(-l)]與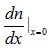 之間的關系。
之間的關系。
這里可以用到Taylor展開,簡單解釋如下(想直接看推導結果的伙伴可以跳到結果):
如果一個函數f(x)在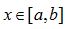 區間具有n階導數fn(x),且已知在
區間具有n階導數fn(x),且已知在![]() 點的值f(x0),那么f(x)可以展開為多項式之和:
點的值f(x0),那么f(x)可以展開為多項式之和:
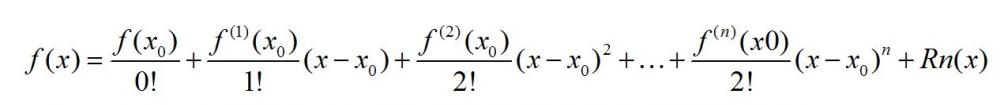 其中,Rn(x)是余項,即誤差項,是(x-x0)n的高階無窮小。具體推導這里不做贅述,簡言之就是可以將任一可求導的函數展開為一個多項式之和,基本規律是x距離x0越近,那么可取的多項式指數也可以越小,誤差也越小(極限情況就是取x=x0,上式就變成f(x)f(x0)。
其中,Rn(x)是余項,即誤差項,是(x-x0)n的高階無窮小。具體推導這里不做贅述,簡言之就是可以將任一可求導的函數展開為一個多項式之和,基本規律是x距離x0越近,那么可取的多項式指數也可以越小,誤差也越小(極限情況就是取x=x0,上式就變成f(x)f(x0)。
回到擴散電流的推導,因為平均自由程顯然是一個微小量(通常為數埃到數百埃,顯然半導體中雜質、缺陷越小,平均自由程越大),利用Taylor展開式,可以將n(l)在x=0處展開為:
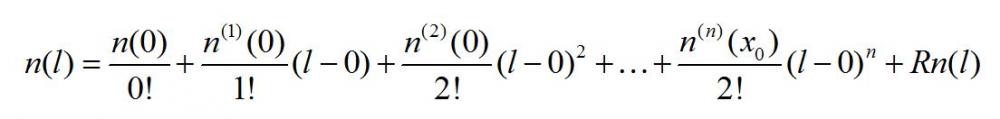 在假設l是一個足夠小的量的情況下,忽略上式中二次方及以上的多項表達式以及誤差項,近似得到:
在假設l是一個足夠小的量的情況下,忽略上式中二次方及以上的多項表達式以及誤差項,近似得到:
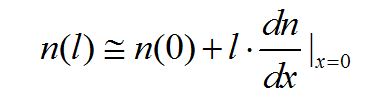
同理:
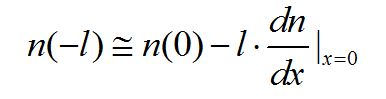

由此我們得到[n(l)-n(-l)]與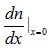 之間的關系。
之間的關系。
結合前面的電流密度推結論![]() ,從而得到:
,從而得到:
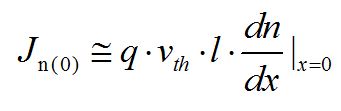
擴展到所有x,有:
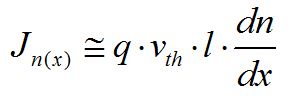
定義電子擴散系數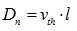 ,就得到大家常見的電子擴散電流方程:
,就得到大家常見的電子擴散電流方程:
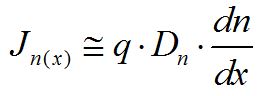
同理,可得到空穴擴散電流方程:
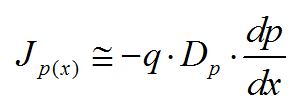
從而,擴散總電流為:
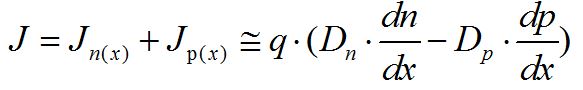
注意:
1.此處在擴散電流的表達式中采用了“約等于”的符號,而絕大多數文獻中是直接為等號。從推導過程中,大家容易發現Taylor展開中是作了近似處理。需要知道的是:當半導體晶體質量越高、摻雜濃度越低,這個表達式的精確度也就越差,就需要引入更高階的多項式來減小誤差。
2.擴散電流中的速度是Vth一個統計值,也就是說與漂移電流不同的是,擴散電流等式不適用于單個電荷等不具有統計意義的對象。
至此,我們已分別推導得到漂移電流和擴散電流的表達式,那么半導體中的電荷移動所產生的總電流即為兩者之和,即:
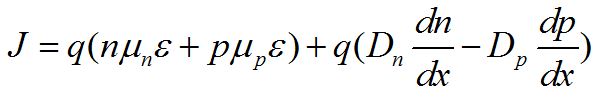
請注意,自此之后,對于上式的使用,我們不再采用“ ”,也就是默認平均自由程足夠小,Taylor展開的一階表達式精度已經足夠。
”,也就是默認平均自由程足夠小,Taylor展開的一階表達式精度已經足夠。
其中,![]() ,
, ![]() 分別為電子和空穴在電場作用下的漂移速度;
分別為電子和空穴在電場作用下的漂移速度;![]() ,
,![]() 分別為電子和空穴在存在濃度梯度情況下的擴散速度。
分別為電子和空穴在存在濃度梯度情況下的擴散速度。
由此,我們達到了本章開篇所述之目的——“梳理清楚了速度與濃度梯度以及電場的關系,自然也就梳理楚了擴散運動以及漂移運動分別形成的電流,而兩者之和就是總的電流”。
文末總結
1、在一維情況下,電流J與速度v之間的關系:
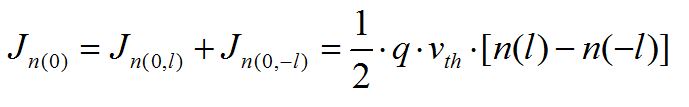
2、電流J、速v和濃度梯度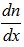 之間的關系:
之間的關系:
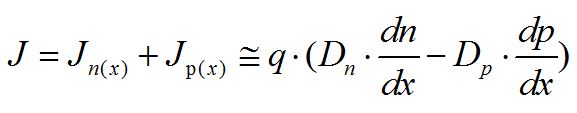
3、半導體中的電荷移動所產生的總電流:
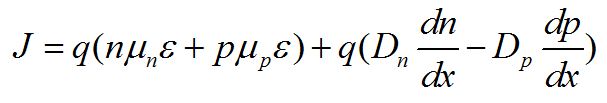
*博客內容為網友個人發布,僅代表博主個人觀點,如有侵權請聯系工作人員刪除。