改進的D-S理論在ETC系統中的應用研究
1 D-S 證據理論概述及改進
Dempster-Shafer 證據理論(簡稱D-S 證據理論)源于20 世紀60 年代Dempster 在多值映射方面的工作,他將證據的信任函數與概率空間的概率的最大最小值相關聯,構造了不確定推理模型的一般框架。此后Shafer 又在此基礎上進行了擴展,形成了能夠處理不確定、不精確、不完整信息的證據理論。它憑借其能夠表示“不確定性”、“未知”等概念的優點,在數據融合中得到廣泛重視。
1.1 D-S 證據理論概述
設有一個有限假設空間,Θ為空間中所有命題的窮舉集合,D-S 理論用“識別框架(Frame. of Discernment)”描述構成整個假設空間的所有命題的集合Θ,識別框架中的各元素要求互相排斥,而集合中的命題稱為識別框架的原命題。定義1 設Θ為給定識別框架,Ω=2Θ為Θ的冪集,則函數m:Ω→[0,1],在滿足下列條件:
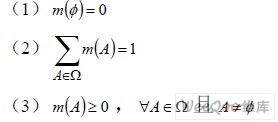
時,稱m 為Ω 上的基本概率分配;?A∈Ω,m(A)稱為基本概率分配函數(BPA),m(A)≥0的命題稱為證據的焦元。
定義2 設Θ 為一識別框架,m(A)為Ω 上的基本概率分配函數,滿足下列的函數稱為信任函數:
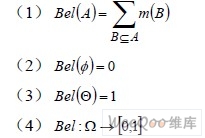
其中A 的信度函數為A 中每個子集的信度之和,Bel(A)表示對A 的總的信任程度,亦為可信度。
定義3 Bel 為給定信任函數,有一函數PL:
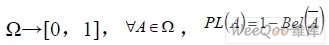
,則PL為A 的似然函數。即:

雖然D-S 證據理論在實際得到廣泛的追捧,但在應用中人們發現其自身也存在一些不足和缺點,特別是在高沖突證據組合的時候會導致合成的結果違背直覺。前人如Zadeh 和Yager、Smets 他們也在這個問題上做了許多詳細的研究,并提出了針對性的意見及妥善的改進方法。可惜隨著科技的進步這一問題終究沒有得到很好的解決。
1.2 D-S 證據理論的改進
D-S 的合成法則如下:
m1 與m2 是識別框架Θ 的兩個獨立證據,Ω 為Θ 的冪集,A、B 為冪集中的元素,則這兩個證據組合后得到的組合證據為:

其中
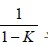
為歸一化常數:
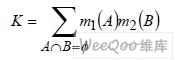
它的作用就是避免在合成時將非零的概率賦給空集Φ。
雖然D-S 理論有諸多優點,但在實際的應用中卻不是令人滿意,往往有時與直覺相違背,主要的原因是存在證據沖突,這是不可小覷的問題。所以做了如下的改進,取沖突權值為歸一化常數的對數:

如果上述兩個證據之間不存在沖突,則Cov(Bela,Belb)=∞;如果證據間完全沖突,則Cov(Bela,Belb)=0。在充分認識到證據間的沖突下,令σ=1-K 為沖突因子,當σ=0 時證據之間不存在任何沖突,當σ=1 時證據之間完全沖突,那么對D-S 的合成法則改進如下:
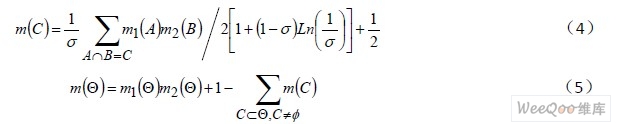
當融合的證據信息多于兩個以上時,σ1,σ2,…,σn 為各個證據之間的沖突因子,則有:
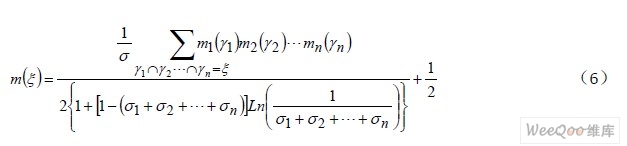



評論